Pointer Analysis

Motivation
Introduction to Pointer Analysis
Key Factors of Pointer Analysis
Concerned Statements

Motivation

via CHA

void foo(){
	Number n = new One()
	int x = n.get();
}

interface Number{
	int get();
}

class Zero implements Number{
	public int get(){
		return 0;
	}
}

class One implements Number{
	public int get(){
		return 1;
	}
}

class Two implements Numebr {
	public int get(){
		return 2;
	}
}

存在如上的示例代码，如果用CHA，那么n.get()根据Number类，会得到的target method是：{Zero.get(), One.get(), Two.get()}；

根据常量传播的分析，x=NAC，因为0,1,2三个值都返回，merge时则为NAC；

因此在这种情况中，使用CHA的常量传播算法就丢失了精度；

如果用指针分析来分析程序呢？

via Pointer Analysis

void foo(){
	Number n = new One()
	int x = n.get();
}

简单来说，由于n.get()的调用，根据指向的对象One，因此可以精确地得到target method：{One.get()}；

因此可以准确地到返回值1；

Introduction to Pointer Analysis

A fundamental static analysis
- Computes which memory locations a pointer can point to - 计算指针指向内存的位置
For object-oriented programs(focus on Java)
- Computes which objects a pointer(variable or field) can point to - 计算指针指向的对象
Regarded as a may-analysis
- Computes an over-approximation of the set of objects that a pointer can point to, i.e., we ask “a pointer may point to which objects?” - 指针指向了哪些对象

Example

// Sample 2
void foo(){
	A a = new A();
	B x = new B();
	a.setB(x);
	B y = a.getB();
}

class A {
	B b;
	
	void setB(B b){
		this.b = b;
	}

	B getB(){
		return this.b;
	}
}

存在以上程序，通过指针分析，输入上面的程序，得到对应的表格：

Variable	Object
a	new A
x	new B
this	new A
b	new B
y	new B

Field	Object
new A.b	new B

那么如何通过程序来得到这样的表格呢？

Alias Analysis

这里引出了一种分析–Alias analysis

Two closely related but different concepts

Pointer analysis: which objects a pointer can point to?
Alias anlaysis: can two pointers point to the same object?

If two pointers, say p and q, refer to the same object, then p and q are aliases

p = new C();
q = p;
x = new X();
y = new Y();

上面的例子可以得出，p和q是aliases，而x和y则不是；

Applications of Pointer Analysis

Fundamental information
- Call graph
- aliases
- …
Compiler optimization
- Virtual call inlining
- …
Bug detection
- Null pointer detection
- …
Security anlaysis
- Information flow analysis
- …
And many more…

Key Factors of Pointer Analysis

Pointer analysis is a complex system
Multiple factors affect the precision and efficiency of the system

Factor	Problem	Choice
Heap abstarction	How to model heap memory?	- Allocation-site - Storeless
Context sensitivity	How to model calling contexts?	- Context-sensitive - Context-insensitive
Flow sensitivity	How to model control flow?	- Flow-sensitive - Flow-insensitive
Analysis scope	Which parts of program should be are analyzed?	- Whole-program Demand-driven

Heap Abstraction

How to model heap memory?

In dynamic execution, the number of heap objects can be unbounded due to loops and recursion
for (...){
A a = new A();
}
To ensure termination, heap abstraction models dynamically allocated, unbounded concrete objects as finite abstract objects for static analysis

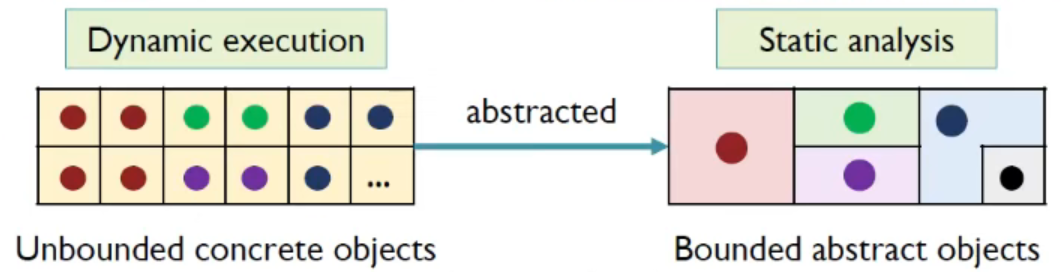
为了确保循环或者其他原因产生无穷尽的内存堆块（这样就不好进行静态分析），使用抽象的方法将具有共性的对象抽象到一起，形成有限的处理单元，保证静态分析能够终止；

对于Heap Abstraction，有两大方向，其中又有很多小的方向：

Store based model
- k-limiting
- Allocation sites
- …
Storeless model
- k-limiting
- Patterns
- …

这里只学习Allocation sites；

Allocaiton sites(selected)

The most commonly-used heap abstraction

Model concrete objects by their allocaiton sites
One abstract object per allocation site to present all its allocated concrete objects

有一个例子：

for(i = 0; i < 3; ++i){
	a = new A();
	...
}

对于上述代码，for循环执行了三次，创建了三个对象；

这里规定，使用$O_i$代表程序第$i$行的创建点$O$。

根据这个规则能够得到：

$O_2$,iteration i = 0

$O_2$,iteration i = 1

$O_2$,iteration i = 2

如果用allocation-site abstraction的技术进行分析，则只得到一个创建点的抽象$O_2$

The number of allocation sites in a program is bounded, thus the abstract objects must be finite.

Context Sensitivity

How to model calling contexts? - 指针分析的过程中如何对调用的上下文进行建模？

通常有两种选择，针对：

context-sensitive	context-insensitive
Distinguish different calling contexts of a method	Merge all calling contexts of a method
Analyze each method multiple times, once for each context	Analyze each method once

context-sensitive(selected)

一个方法可能会被调用很多次，产生不同的上下文，需要进行区别
对一个方法分析多次，每一个上下文分析一次

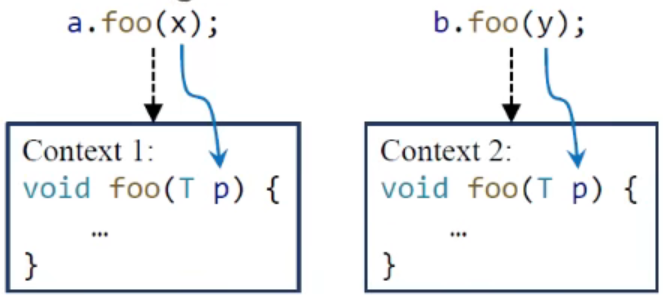
上面的例子说明，当一个方法调用两次时，由于实体对象不同，针对上下文敏感分成了两个context；

context-insensitive(selected)

对于一个方法，产生的上下文merge到一起（可能丢失精度）

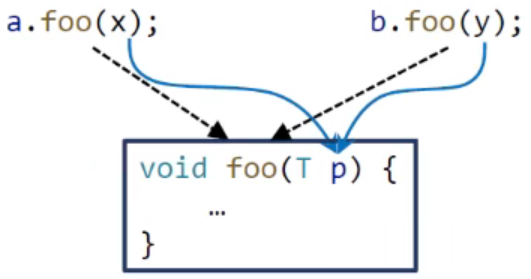
上面的例子说明，当一个方法调用两次时，虽然实体对象不同，但是上下文不敏感，因此都指向了同一个context；

Flow Sensitivity

How to model control flow?

Flow-sensitive	Flow-insensitive
Respect the execution order of the statements	Ignore the control-flow order, treat the program as a set of unordered statements
Maintain a map of points-to relations at each program location	Maintain one map of points-to relations for the whole program.

在指针分析的过程中，如何对程序控制流进行建模；

可以分为对控制流敏感和不敏感的情况进行分析；

1: c = new C();
2: c.f = "x";
3: s = c.f;
4: c.f = "y";

Flow-sensitive

流敏感的分析会尊重程序语句的先后顺序，在程序语句的每一行都会建立一个点，用来做指针映射指向；

对于上面例子，流敏感分析可以得到结果：

1: c -> {$O_1$}

2: c -> {$O_1$}, $O_1$.f -> {“x”}

3: c -> {$O_1$}, $O_1$.f -> {“x”}, s -> {“x”}

4: c -> {$O_1$}, $O_1$.f -> {“y”}, s -> {“x”}

Flow-insensitive(selected)

忽视控制流的顺序，当做无序程序语句的集合

c -> {$O_1$}, $O_1$.f -> {“x”, “y”}, s -> {“x”, “y”}

存在语言间的效率差别，java中使用insensitive进行指针分析并没有相对于sensitive效率差很多；

Analysis Scope

Which parts of program should be analyzed?

Whole-program	Demand-driven
Coompute points-to information for all pointers in the program	Only compute points-to information fot the pointers that may affect specific sites of interest(on demand)
Provide information for all possible clients	Provide information for specific clients

x = new A();
y = x;
y.foo();
z = new T();
z.bar();

Whole-program(selected)

分析整个程序中的指针

以上面的代码为例，将所有的指针进行分析：

x -> {$O_1$}

y -> {$O_1$}

z -> {$O_4$}

Demand-driven

根据需求驱动，只分析满足特定应用的指针

如果根据需求：

Client: call graph construction
Site of interest: line 5

我们需要收集的信息是：

z = new T();
z.bar();

得到的结果为：z -> {$O_4$}

虽然只需要一些指针信息，但是也需要保证结果是safe的，需要将程序的很大一部分分析完，才能找到依赖的信息，所以效率并不一定比whole-program的方式高。另外client的需求有可能多样化，每次分析可能会有重复；

Concerned Statement

What do we analyze?

在进行指针分析时，只关注的是pointer-affecting statements，即影响指针的一些语句；

Pointers in Java

Local variable: x
Static field: C.f
Instance field: x.f
Array element: array[i]

static_program_analysis_06_pointer_analysis