Data Flow Analysis – Foundations

Iterative Algorithm, another view
Partial Order
Upper and Lower Bounds
Lattice, Semilattice, Complete and Product Lattice
Data Flow Analysis Framework via Lattice
Monotonicity and Fixed Point Theorem
Relate Iterative Algorithm to Fixed Point Theorem
May/Must Analysis, A Lattice View
Distributivity and MOP
Constant Propagation
Worklist Algorithm

涉及到：数学理论和证明，内容概念抽象而繁杂。

Iterative algorithm

This general iterative algorithm produces a soluiton to data flow analysis.

For May&Forward Analysis

OUT[entry] = ∅
OUT[B]=∅
$OUT[B] = IN[B]=∪_{P \space a \space predecessor \space of \space B}OUT[P], \space gen_B \space ∪ \space (IN[B] - kill_B) $

这是上一节课所总结的内容，现在从另一个角度来分析；

View Iterative Algorithm in Another Way

Given a CFG(program) with k nodes, the iterative alogrithm updates OUT[n] for every node n in each iteration
Assume the domain of the values in data flow analysis is V, then we can define a k-tuple.
$$
(OUT[n_1], OUT[n_2], … ,OUT[n_k])
$$
as an element of set ($V_1 × V_2 × …×V_k$) denoted as $V^k$, to hold the values of the analysis after each iteration.
Each iteration can be considered as taking an action to map an elemtn of $V^k$ to a new element of $V^k$, through applying the transfer functions and control-flow handing, abstracted as a function $F:V^k$->$Vk$
Then the algorithm outputs a series of k-tuples is the same as the last one in two consecutive iterations.

Sample

可以看到：

红色部分的代码可以视为初始化的过程；

init => (⊥, ⊥, …, ⊥) = $X_0$

(⊥, ⊥, …, ⊥)是一个k-tuple，用bottom表示其元素；
黄色部分的代码作为迭代的条件

when

iter i => (${v_1}^i,{v_2}i,…,{v_k}^i$) = $F(X_{i-1})$

exists

iter i+1 => (${v_1}^{i},{v_2}{i},…,{v_k}^{i}$) = $F(X_i)$

即：

$X_i = X_{i+1}$ => $X_i=X_{i+1}=F(X_i)$

则达到不动点，退出循环；
绿色部分的代码迭代的操作

iter 1 => (${v_1}^1,{v_2}1,…,{v_k}^1$) = $X_1$ = $F(X_0)$

iter 2 => (${v_1}^2,{v_2}2,…,{v_k}^2$) = $X_2$ = $F(X_1)$

…

iter i => (${v_1}^i,{v_2}i,…,{v_k}^i$) = $X_i$ = $F(X_{i-1})$

由此得到的结论是：

$X$ is a fixed point of function $F$ if $X=F(X)$ => The iterative algorithm reaches a fixed point.

partial means for a pair of set elements in P, they could be incomparable; in other words, not necessary that every pair of set elements must statisfy the ordering $\sqsubseteq$. 不一定所有元素都需要满足.

Some Question

The iterative alogrithm (or the IN/OUT equation system) produces a solution to a data flow analysis

Is the algorithm guaranteed to terminate orreach the fixed point, or does it always have a soluiton?

所有的data flow的分析都可以使用吗，一定都能达到不动点吗？
If so, is there only one solution or only one fixed point? If more than one, is our solution the best one(most precise)?

如果不动点成立，它只有一个吗，是最精确的吗？
When will the algorithm reach the fixed point, or when can we get the solution?

什么时候能到不动点？

Partial Order

偏序集poset(PartiallyOrdered set), We define poset as a pair(P, $\sqsubseteq$) where $\sqsubseteq$ is a binary relation that defines a partial ordering over P, and $\sqsubseteq$ has the following properties:

(1) Reflexivity自反性: $\forall x \in P, x \sqsubseteq x$

(2) Antisymmetry反对称性$\forall x,y \in P,x \sqsubseteq y \land y \sqsubseteq x $ => $x=y$

(3) Transitivity传递性$\forall x,y,z \in P, x \sqsubseteq y \land y \sqsubseteq z$ => $x \sqsubseteq z$

满足这三个性质的set为poset

Sample 1

Is ($S, \sqsubseteq$) a poset where S is a set of integers and $\sqsubseteq$ representes $\leq$ (less than or equal to)?

当S是整数集合时，S是poset吗？

(1) Reflexivity: 1 <= 1, 2 <= 2

(2) Antisymmetry: 1 <= 1 $\land$ 1 <= 1 then 1 = 1

(3) Transitivity: 1 <= 2 $\land$ 2 <= 3 then 1 <= 3

因此$S$为opset；

Sample 2

Is ($S, \sqsubseteq$) a poset where S is a set of integers and $\sqsubseteq$ representes $<$ (less than)?

当S是整数集合时，S是poset吗？

(1) Reflexivity: 1 < 1, 2 < 2 ----不满足

Sample 3

Is ($S, \sqsubseteq$) a poset where S is a set of English words and $\sqsubseteq$ representes the substring relation, i.e., $s1\sqsubseteq s2$ means s1 is a substring of s2?

当S是满足上述条件的英文单词集合，S是opset吗？

S such as :

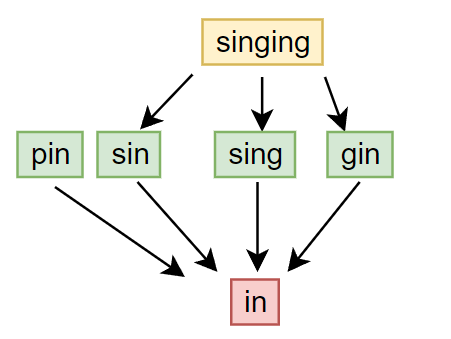
(1) Reflexivity: 每个string是否为自己的substring？符合

(2) Antisymmetry: string是自己的substring，反过来还是。符合

(3) Transitivity: in $\in$ sing, sing $\in$ singing => in $\in$ singing 符合

Upper & Lower Bounds

Given a poset(P,$\sqsubseteq$) and its subset S that S $\subseteq$ P, we say that u $\in$ P is an upper bound of S, if $\forall x \in S, x \sqsubseteq u$.Similarly, we say that l $\in$ P is an lower bound of S, if $\forall x \in S, l \sqsubseteq x$.

Sample 1

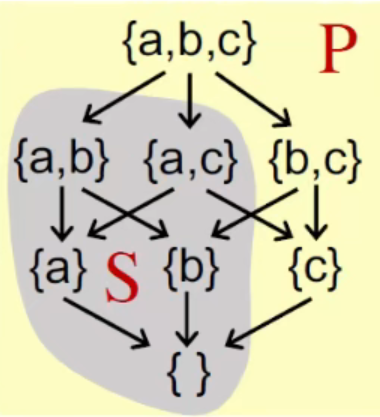
对于S：

upper bound => {a, b, c}

lower bound => {}

We define the least upper bound 最小上界(lub or join) of S, written $\sqcup$S, if for every upper bound of S, say u, $\sqcup$S $\sqsubseteq$ u. Similarly, We define the greatest lower bound 最大下界(glb or meet) of S, written $\sqcap$S, if for every upper bound of S, say l, l $\sqsubseteq$ $\sqcap$S.

Sample 2

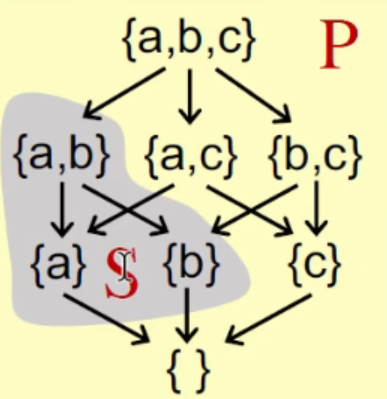
对于S：

upper bound => {a, b, c}, {a, b}

least upper bound (join or lub,) => {a, b}

lower bound => {}

greast lower bound (meet or glb, ) => {}

Properties

Not every poset has lub or glb
But if a poset has lub or glb, it will be unique

Proof.

assume $g_1$ and $g_2$ are both glbs of poset P according to the definition of glb
$$
g_1 \sqsubseteq (g_2 = \sqcap P) ,\space g_2 \sqsubseteq(g_1 = \sqcap P)
$$
by the antisymetry of partiallyordered set => $\sqsubseteq g_1=g_2$

Lattice

Given a poset(P, $\sqsubseteq$), $\forall a, b \in P, if \space a \sqcup b$ and $a \sqcap b$ exists, then (P, $\sqsubseteq$) is called a lattice.

A poset is a lattice if every pair of its elements has a least upper bound and ag reatest lower bound.

Sample 1

Is(S, $\sqsubseteq$) a lattice where S is a set of integers and $\sqsubseteq$ represents <= (less than or equal to)?

The $\sqcap$ operator means “min”, The $\sqcup$ operator means “max”. so yes.

Sample 2

Is ($S, \sqsubseteq$) a lattice where S is a set of English words and $\sqsubseteq$ representes the substring relation, i.e., $s1\sqsubseteq s2$ means s1 is a substring of s2?

必须要满足任意元素的最小上界和最大下界都存在，但是pin和sin显然没有共同的最小上界。 so no.

Sample 3

sample_4

The $\sqcap$ operator means $\cap$, The $\sqcup$ operator means $\cup$. so yes.

Semilattice

Given a poset(P, $\sqsubseteq$), $\forall a, b \in P$,

if only $a \sqcup b$ exists, then (P, $\sqsubseteq$) is called a join semilattice.

if only $a \sqcap b$ exists, then (P, $\sqsubseteq$) is called a meet semilattice.

Complete Lattice

Given a lattice(P, $\sqsubseteq$), for arbitrary subset S of P, if $\sqcup S$ and $\sqcap S$ exist, then (P, $\sqsubseteq$) is call a complete lattice.

All subsets of a lattice have a least upper bound and a greatest lower bound.

Sample 1

Is(S, $\sqsubseteq$) a complete lattice where S is a set of integers and $\sqsubseteq$ represents <= (less than or equal to)?

For a subset $S^+$ including all positive integers, it has no $\sqcup S^+$($+\infty$)

整数集本身是无穷的，无边界的。

Sample 2

sample_4

Yes. The definition of bounds implies that the bounds are not necessarily in the subsets(but they must be in the lattice)

Top & Bottom

Every complete lattice (P, $\sqsubseteq$) has

a greatest element T = $\sqcup P$ called top

a least elemtent ⊥ = $\sqcap P$ called bottom

Every finite lattice (P is finite) is a complete lattice. 有穷格是完全格，但是完全格不一定是有穷格（0,1之间的实数集）。

Product Lattice

Given lattices $L_1=(P_1, \sqsubseteq_1),L_2=(P_2,\sqsubseteq_2),…,L_n=(P_n,\sqsubseteq_n)$, if for all i, $(P_i, \sqsubseteq_i)$has $\sqcup_i$(least upper bound) and $\sqcap_i$(greatest lower bound), then we can have a product lattice $L^n = (P, \sqsubseteq)$ that is defined by:

值域：$ P = P_1 × P_2 × \space … \space × P_n$

two element to opset：$(x_1, \space … \space x_n ) \sqsubseteq (y_1, \space … \space y_n)$ <=> $(x_1 \sqsubseteq y_1) \and … \and (x_n \sqsubseteq y_n)$

下界关系：$(x_1, \space … \space x_n ) \sqcup (y_1, \space … \space y_n)$ = $(x_1 \sqcup_1 y_1, … , (x_n \sqcup_n y_n)$

上界关系：$(x_1, \space … \space x_n ) \sqcap (y_1, \space … \space y_n)$ = $(x_1 \sqcap_1 y1 , … , (x_n \sqcap_n y_n)$

A product lattice is a lattice

If a product lattice L is a product of complete lattices, then L is also complete

Data Flow Analysis Framework via Lattice

A data flow analysis framework (D, L, F) consists of:

D：a direction of data flow: forwards or backwards

L：a lattice including domain of the values V and a meet $\sqcap$ or join $\sqcup$ operator

F：a family of transfer funcitons from V to V

Sample

对于如上的例子，先看左边，

假设已知：
- Direction: Forward
- Merge: Union
- OUT[s1]={a}， OUT[s3]={b}
可以得到：
- IN[s2]={a,b}；

那么以上操作对应右侧，有：

May Analysis从bottom开始：
- 初始化空{}，对应a,b,c的subset为{0,0,0}；
- OUT[s1],OUT[s3]得到的IN[S2]={a,b}，是一个向上汇聚的过程

而由IN到OUT需要做一个F: tansfer function操作；

Data flow analysis can be seen as iteratively applying transfer functions and meet/join operations on the values of a lattice

Review the questions

Is the algorithm guaranteed to terminate orreach the fixed point, or does it always have a soluiton?

所有的data flow的分析都可以使用吗，一定都能达到不动点吗？
- Recall “OUT never shrinks” It is about monotonicity. Lattice上的单调性问题。
- 关联问题？Now what we have just seen is the property(fixed point theorem) for the function on a lattice. We cannot say our iterative algorithm also has that property unless we can relate the algorithm to the fixed point theorem, if possible.
If so, is there only one solution or only one fixed point? If more than one, is our solution the best one(most precise)?

如果不动点成立，它只有一个吗，是最精确的吗？
- 对于$X=F(X)$的函数不动点，一个函数可以有多个不动点。还有一个问题待解决。Iterative algorithm 从初始化开始递归，需要走到哪一个不动点？哪一个精确呢？
When will the algorithm reach the fixed point, or when can we get the solution?

什么时候能到不动点？

Monotonicity

A function f: L -> L (L is a lattice) is monotonic if $\forall x, y \in L, x \sqsubseteq y$ => $f(x) \sqsubseteq f(y)$

Fixed-Point Theorem

Given a complete lattice(L, $\sqsubseteq$), if:

f: L -> L is monotonic & L is finite,

前提是：全格 + 单调 + 有限

then,

the least fixed point of f can be found by iterating

$f(⊥), f(f(⊥)), … ,f^k(⊥)$ until a fixed point is reached

单调 + 由⊥迭代 => 最小不动点

the greastest fixed point of f can be found by iterating

$f($T$)$, $f(f($T$))$, … ,$f^k($T$)$ until a fixed point is reached

单调 + 由T迭代 => 最大不动点

若要证明最小不动点成立，需要证明：

不动点存在
不动点最小

若要证明最大不动点成立，需要证明：

不动点存在
不动点最大

Existence of Fixed Point

如何证明不动点的存在？

Proofs.

Bt the definition of ⊥ and f: L -> L, we have
$$
⊥ \sqsubseteq f(⊥),\space f(⊥) \in L
$$
As f is monotonic, we have
$$
f(⊥) \sqsubseteq f(f(⊥)) = f^2(⊥),\space f(⊥) \sqsubseteq f^2(⊥)
$$

$$
f(⊥) \in L, \space f^2(⊥) \in L
$$

Similarly (by repeatedly applying f), we have
$$
⊥ \sqsubseteq f(⊥) \sqsubseteq f^2(⊥) \sqsubseteq … \sqsubseteq f^i(⊥)
$$
As L is finite, for some k, we have
$$
f^{Fix} = f^k(⊥) = f^{k+1}(⊥)
$$
Thus, the fixed point exists.

Least Fixed Point

证明最小不动点？

Proof.

Assume we have another fixed point x, i.e., x = f(x)

By the definition of ⊥, we have ⊥ $\sqsubseteq $ x

Induction begins:

As f is monotonic, we have
$$
f(⊥) \sqsubseteq f(x)
$$
Assume $f^i(⊥) \sqsubseteq f^i(x)$, as f is monotonic, we have
$$
f^{i+1}(⊥) \sqsubseteq f^{i+1}(x)
$$
Thus by induction, we have
$$
f^i(⊥) \sqsubseteq f^i(x)
$$
Thus $f^i(⊥) \sqsubseteq f^i(x)=x$, then we have
$$
f^{Fix}=fk(⊥) \sqsubseteq x
$$
Thus the fied point is the least.

Greatest Fixed Point

参考最小不动点的证明，可以得到：
$$
x \sqsubseteq f^k(⊥)=f{Fix}
$$

Relate Iterative Algorithm to Fixed-Point Theorem

如何关联呢？

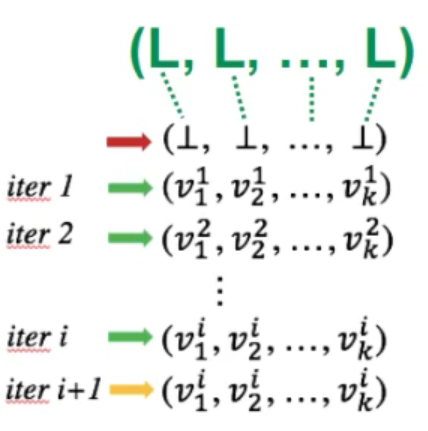
If a product lattice $L^k$ is a product of complete (and finite) lattices, i.e., (L, L, …, L), then $L^k$ is also complete (and finite)

In each iteration, it is equivalent to think that we apply function F which consists of

transfer function f: L -> L for every node <=> 对于每个node应用transfer function

join/meet function $\sqcap$/$\sqcup$: L × L -> L for control-flow confluence <=> merge时进行处理，应用join或meet

已经证明了是有限的，现在需要证明的是function F是否是单调的。

$Gen, Kill$ function is monotonic => transfer function is monotonic

Is join/meet function monotonic?

To prove join is monotonic =>

Proof.

$\forall x, y, z \in L, \space x \sqsubseteq y$, we want to prove $x \sqcup z \sqsubseteq y \sqcup z$ => 意味着进行join操作后，仍然满足单调关系

by the definition of $\sqcup, \space y \sqsubseteq y \sqcup z$ => join求的是两个元素的最小上界，所以 y join z 会满足$\space y \sqsubseteq y \sqcup z$

by transitivity of $\sqsubseteq, \space x \sqsubseteq y \sqcup z$ => 由于$x \sqsubseteq y$，根据传递性，可以得到$x \sqsubseteq y \sqsubseteq y \sqcup z$

thus $y \sqcup z$ is an upper bound for x, and also for z (by $\sqcup$'s definition) => $y \sqcup z$为x的上界，y和z的最小上界

as $x \sqcup z$ is the least upper bound of x and z => $x \sqcup z$是x,z的最小上界，最小上界小于$y \sqcup z$(上界)

thus $x \sqcup z \sqsubseteq y \sqcup z$

同理可证meet；

When will the algorithm reach the fixed point?

The height of a lattice $h$ is the length of the longest path from Top to Bottom in the lattice.

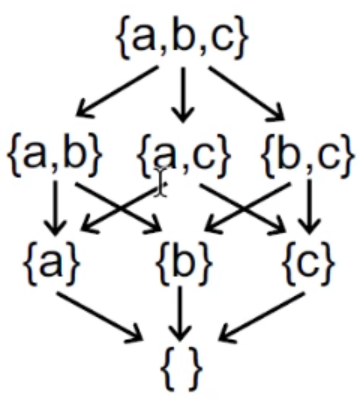
对于上图的例子而言，其高度$h=3$；

现在需要求得到不动点需要的迭代次数$i$；

在每次迭代中，假设往一个方向上的每一次迭代只有一个结点的变化，例如0->1。

假设lattice高度为h，而结点个数为k，最坏情况下，相当于每一个结点从空到"满"，从bottom->top，每一个结点需要处理h次，则需要的迭代次数为h*k；

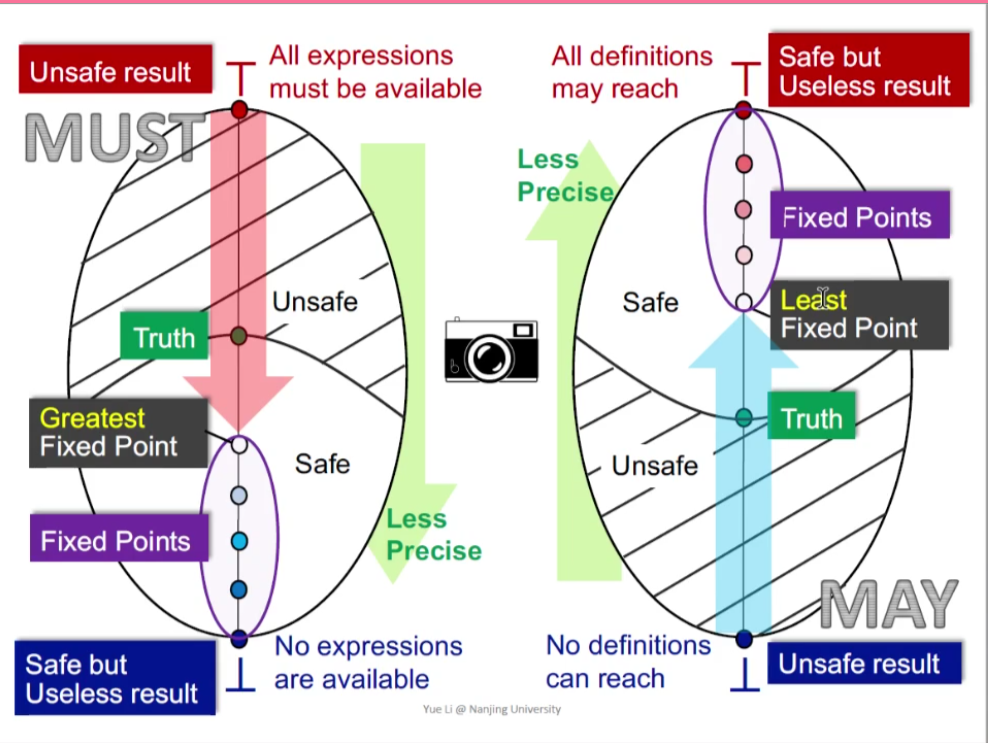
May&Must Analysis from a lattice view

通过lattice的角度，用图例说明上述结论。

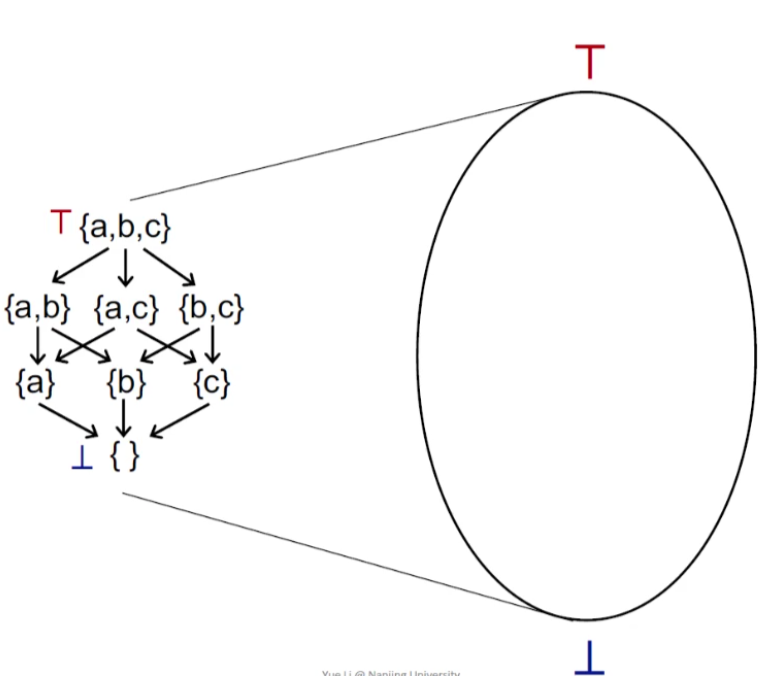
假设lattice是一个product lattice。

May Analysis

目的是：unsafe result -> safe result

例如，Reaching Definition中：

程序开始时即为bottom，处于unsafe result（No definitions can reach所有变量都初始化了，因为作为一个查询错误的程序，所以如果一开始就表述结果为没有错误，就是一个unsafe的结果）。

当处于safe result（All definitions may reach），即查错程序认为程序的变量都有出现了reach的问题，但这是Safe but useless result。因为作为查错程序，需要找出Truth。

查错程序停留在Truth时，即为所需要求得的result。

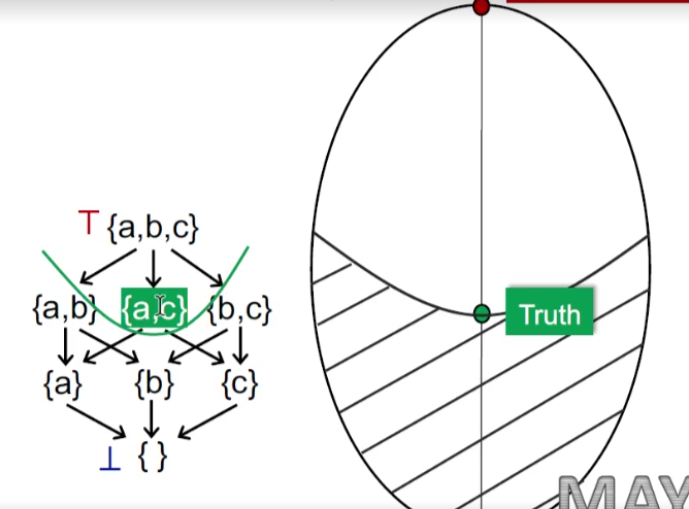
假设一个lattice为上图左边部分所示，{a,c}为Truth，那么Truth上即为safe，而Truth下为unsafe。那么如何知道有没有进入到Safe域。

在求解步骤中存在很多不动点，但是may analysis所求的是最小不动点。

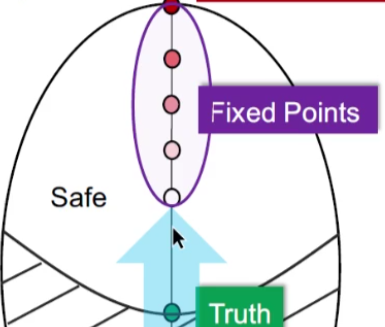
处于精确度的考虑，最小不动点与Truth最相近，因此Least Fixed Point在Fixed Points中最为准确。

Must Analysis

目的是：unsafe result -> safe result

以expressions available的优化程序为例，Top的初始为unsafe(All expressions must be available)，这就相当于程序还没有开始分析优化，就断定所有expression都available，都可以使用，所以是unsafe。

当运行到bottom时，是safe的，相当于所有expression都是不可用，这是一种safe的情况，但是没有相当于不需要再做优化，因此相当于一个safe but useless result。

因为Must Analysis允许漏报，但是不允许误报。如果处于unsafe域，在expressions availble检查中，如果误报，则程序分析会导致错误。

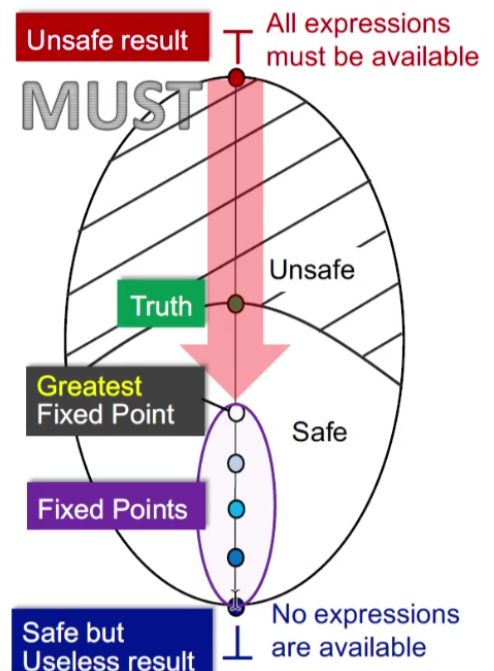
针对与该分析，must Analysis时，到达最大不动点时，进入safe域，最接近truth，因此最为精确。

How Precise is our solution?

Meet-Over-All-Paths Solution (MOP)

A path P from Entry to S：

P = Entry -> S1 -> S2 -> … -> Si ；

$F_P$作为transfer function，对每一个Statement，得出一个OUT，作为下一个statement的IN；

MOP理解起来就是，把多条所有Path的结果join/meet => $MOP[S_i]= \sqcup /\sqcap $

$F_P(OUT[Entry])$

有一些路径不会执行，有一些程序会有循环没有边界，有一些程序路径数量很多，无穷枚举，这些结果不应该被join/meet；

举一个例子：OUR Iterative Alogrithm vs. MOP

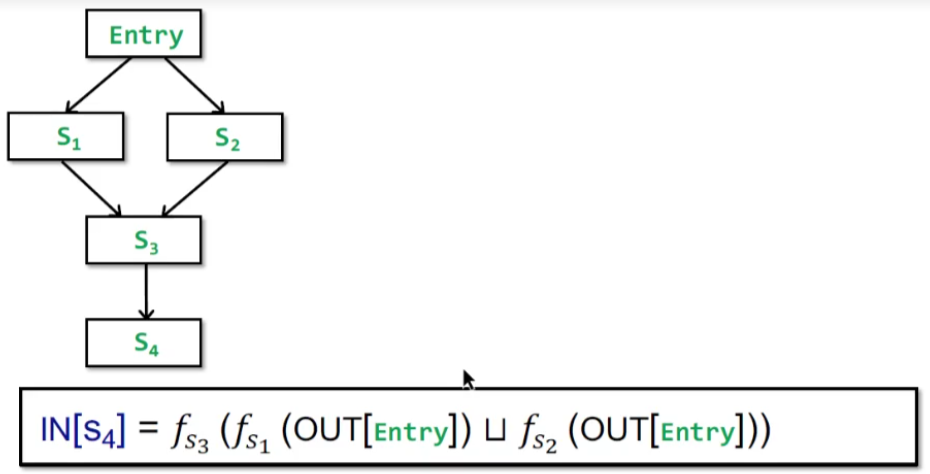
上图是Iterative Alogrithm的做法，merge时join后在使用transfer function处理；

而对于MOP，可以得到

$MOP[S_4]=f_{S_3}(f_{S_1}(OUT[Entry])) \sqcup f_{S_3}(f_{S_2}(OUT[Entry]))$

相当于merge时，先transfer function处理各个分支，再join；

即表示为：
$$
Ours=F(x \sqcup y)
$$

$$
MOP=F(x)\sqcup F(y)
$$

他们之间的关系是什么？

得到$MOP \sqsubseteq Ours$；

当F is distributive，F具有分配性，$F(x \sqcup y)=F(x) \sqcup F(y)$，则有$MOP=Ours$

对于bit-vector or Gen/kill problems，Ours 几乎和MOP一样准；

一个例子：

[Constant Propagation]

Given a variable x at program point p, determine whether x is guaranteed to hold a constant value at p. – must analysis
- The OUT of each node in CFG, includes a set of pairs (x,v) where x is a variable and v is the value held by x after that node.
  A data flow analysis framework(D, L, F)consits of:
  - D: a direction of data flow => [fowards]
  - L: a lattice including domain of the values V and a meet or join operator
  - F: a family of transfer functions from V to V
  - Lattice
    - Domain of the values V
      
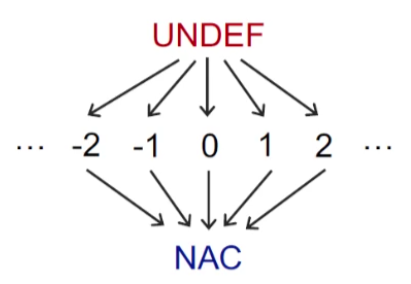
      UNDEF: undefined
      
      NAC: not a constant
    - Meet Operator
      
      NAC $\sqcap$ v = NAC
      
      UNDEF $\sqcap$ v = v
      
      c $\sqcap$ v = ?
      - c $\sqcap$ c = c
      - c1 $\sqcap$ c2 = NAC
  - transfer function
- Nondistributivity
  
  一个例子：

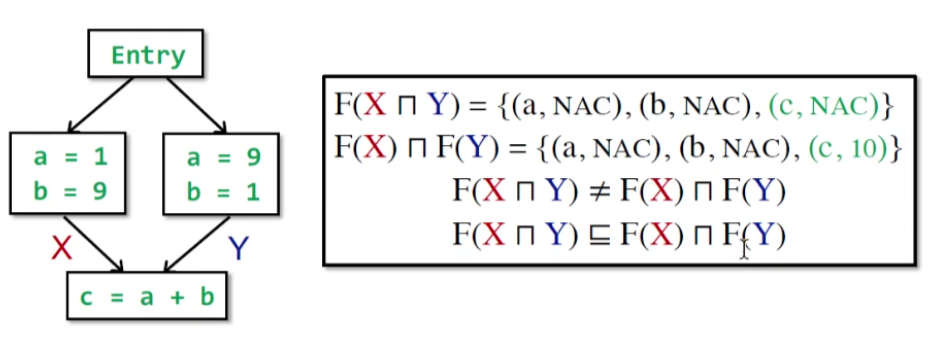
Worklist Alogrithm, an optimization of Iterative Algorithm

Iterative Algorithm在OUT没有变化时才会停止迭代，而worklist algorithm则相反，只处理那些OUT变化的node;

对于Forward Analysis而言，将所有的bb放到worklist中，只要worklist不是空的，则选择一个worklist中的bb来进行transfer操作，如果操作后OUT变化了，则说明后面的bb的IN可能变化了，则将其所有后继加入到worklist中。

Summary

Iterative Algorithm, another view
partial order
upper and lower bounds
lattice, semilattice, complete and product lattice
data flow analysis framework via lattice
monotonicity and fixed point theorem
relate iterative algorithm to fixed point theorem
may/must analysis, a lattice view
MOP and distributivity
constant propagation
worklist algorithm

Key Point

Understand the functional view of iterative algorithm
The definitions of lattice and complete lattice
understand the fixed-point therorem
how to summarize may and must analysis in lattices
The relation between MOP and the solution produced by the iterative algorithm
Constant propagation algorithm
Worklist algorithm

static_program_analysis_04_data_flow_analysis_foundations

Data Flow Analysis – Foundations

Contents

Iterative algorithm

For May&Forward Analysis

View Iterative Algorithm in Another Way

Sample

Some Question

Partial Order

Sample 1

Sample 2

Sample 3

Upper & Lower Bounds

Sample 1

Sample 2

Properties

Lattice

Sample 1

Sample 2

Sample 3

Semilattice

Complete Lattice

Sample 1

Sample 2

Top & Bottom

Product Lattice

Data Flow Analysis Framework via Lattice

Sample

Review the questions

Monotonicity

Fixed-Point Theorem

Existence of Fixed Point

Least Fixed Point

Greatest Fixed Point

Relate Iterative Algorithm to Fixed-Point Theorem

When will the algorithm reach the fixed point?

May&Must Analysis from a lattice view

May Analysis

Must Analysis

How Precise is our solution?

Worklist Alogrithm, an optimization of Iterative Algorithm

Summary

Key Point