Data Flow Analysis

Overview of Data Flow Analysis

What is Data Flow Analysis

May Analysis: Abstraction, Over-approximation is for most static analysis, outpus information that may be true

Must Analysis: Abstraction, Under-approximation is for specific static analysis, outputs information that mast be true

Safe-approximaiton

may analysis - over-approximation
must nanlysis - under-approximaiton

How application-specific Data Flows through the Nodes(BBs/statements) and Edges(control flows) of CFG?

=> different data-flow analysis applications have

=> different data abstraction and

=> different flow safe-approximation strateges, i.e.

=> different transfer functions and control-flow handlings

Preliminaries of Data Flow Analysis

Input & Output States

Each execution of anIR statement transforms an ionput state to a new output state
The input(output) state is associated with the program point before(after) the statement

通俗来讲，对于一个Statement而言，存在输入和输出的状态，使用IN[..]来代表输入状态，OUT[..]来代表输出状态；

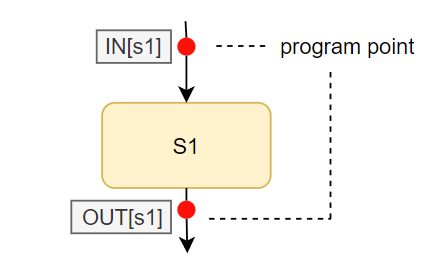
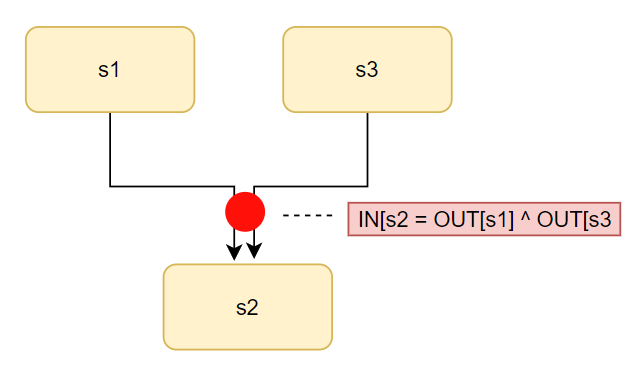
当两个Statement相邻时，上一Statement的Output就是下一个Statement的Input，当两个Statement合并到一个Statement时，需要对两个Statement的Output进行Meet操作，如下：

OUT[s1] ^ OUT[s3] = IN[s2]

In each data-flow analysis application, we associate with every program point a data-flow value that represents an abstraction of the set of all possible program states taht can be observed for that point.

例如：

x = 10;
	---- x = [+] y = [⊥]
y = -1;
	---- x = [+] y = [-]
x = y;
	---- x = [-] y = [-]
x = x / y
	---- x = [+] y = [-]

Nations for Transfer Function’s Constraints

Foward Analysis

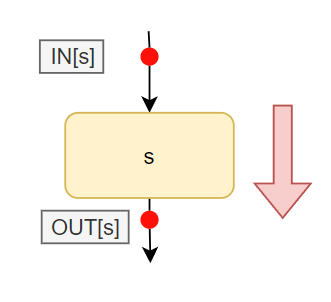使用下面的表示形式来表达上图的Output和input关系

$$
OUT[s] = f_s(IN[s])
$$
Backward Analysis

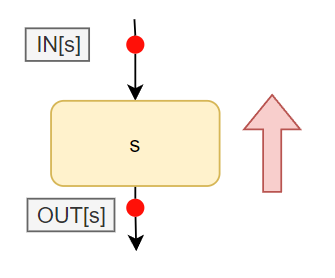使用下面的表示形式来表达上图的逆向的Output和input关系

$$
IN[s] = f_s(OUT[s])
$$

Notations for Control Flow’s Constraints

Control flow within a BB

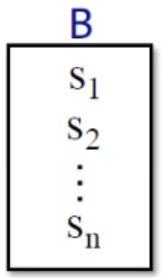
$$
IN[s_{i+1}] = OUT[s_i], for\space all\space i = 1,\space 2,\space …,\space n-1
$$
这个表达式表明，在一个Base Block中，每个statement的输入是它上一个statement的输出。
Control flow among BBs

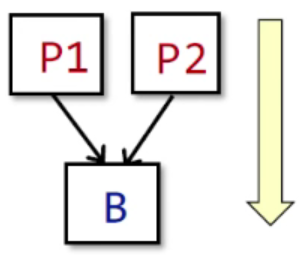
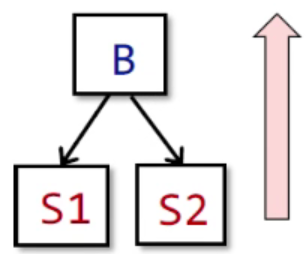
$$
IN[B] = IN[s_1]
\
OUT[B] = OUT[s_n]
\
\
OUT[B] = f_B(IN[B]), \space f_B = f_{s_n} · … · f_{s_2} · f_{s_1}
\
IN[B] = ∧_{P \space a\space predecessor\space of\space B}\space OUT[P]
\
\
IN[B] = f_B(OUT[B]), f_B = f_{s_1} · … · f_{s_{n-1}} · f_{s_n}
\
OUT[B] = ∧_{S \space a\space successor\space of\space B}\space IN[S]
$$

在多个BB之间，存在：
- 当前BB的输入为第一个statement的输入
- 当前BB的输出为该BB中最后一个statment的输出，即第n个statement的输出
- 当P1和P2的OUT为B的IN时，可以用上述的$IN[B] = ∧_{P \space a\space predecessor\space of\space B}\space OUT[P]$表示
- 当反向时也有类似的表示

Data Flow Analysis Applications

Issues Not Covered

下面的内容不包括：

Method Calls - 方法调用
- Intra-procedural CFG
- Will be introduced in lecture: Inter-procedural Analysis
Aliases - 别名，不同变量名指向相同的地址
- Variables have no aliases
- Will be introduced imn lecture: Pointer Analysis

Reaching Definitions Analysis

Preliminary

一个编译优化 - may analysis

A definition d at program point p reaches a point q if there is a path from p to q such that d is not “killed” along that path.

A definition of a variable v is a statement that assigns a value to v - 定义就是对v的声明赋值
Translated as: definition of varibale v at program ponit p reaches point q if there is a path from p to q such that no new definition of v appears on that path - 在p点定义v的位置为d，p->q的路径中，不能对v有新的定义
Reaching definitions can be used to detect possible undefined variables. e.g., introduce a dummy definition for each variablev at the entry of CFG, and if the dummy definition of v reaches a point p where v is used, then v may be used before definition (as undefined reaches v) - 一个变量在定义后，CFG前有一个入口结点，给每一个变量引入一个label，变量在程序执行之前是undefined的，如果这个undefined的值到v被使用的地方，则会报未初始化的错误。显然这是一个may analysis，因为程序有可能会执行到这个路径。

Understanding

D: v = x op y

Data Flow Values/Facts - Abstractoin - 抽象变量的定义
- The definitoins of all the variables in a program
- Can be represented by bit vectors
  
  e.g., D1, D2, D3, D4, …, D100 - 一百个定义抽象为bit
Transfer Function - Safe-approximation
$$
OUT[B] = gen_B \space ∪ \space (IN[B] - kill_B)
$$

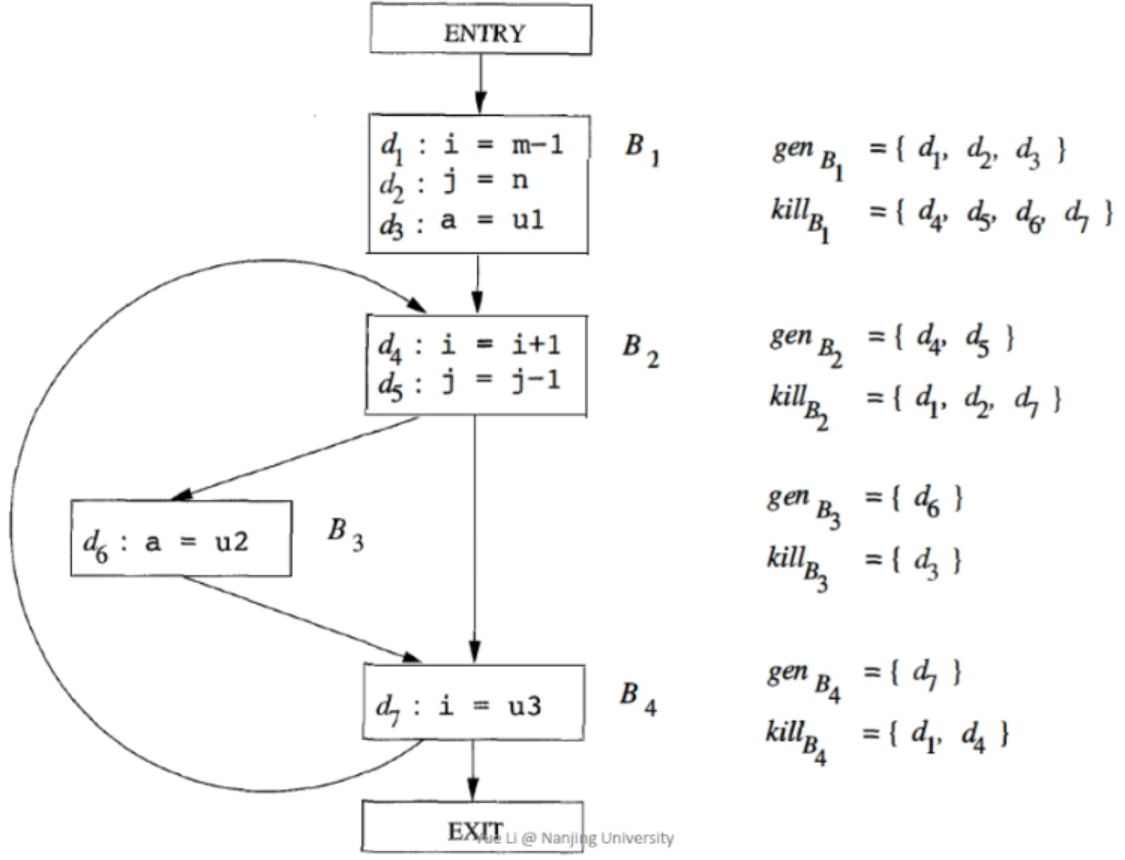
可以看到d1,d2,…,d7都是定义。
- 对于B1：
  - 其$gen_{B_1}$为定义i,j,a三个变量的标志d1,d2,d3；
  - 其$kill_{B_1}$为其他定义i,j,a的其他地方，所以标志为d4,d5,d6,d7；
- 以此类推，可以得到B2的$gen_{B_2}$和$kill_{B_2}$等；
Control Flow
$$
IN[B]=∪_{P \space a\space predecessor\space of\space B}OUT[P]
$$
表示了所有其他前驱所汇聚到IN[B]，形成may analysis的一个过程。

Algorithm

Input: CFG($kill_B$ and $gen_B$ computed for each basic block B)
Output: IN[B] and OUT[B] for each basic block B
Method:
- 第一步，让entry结点的Output为空；
- 然后遍历每一个basic block，让每一个bb的Output为空（这里排除了entry，是因为这是一个算法模板，有其他的算法对entry有其他操作，所以初始化时应当分开来进行）；
- 只要有任何一个bb的Output发生了变化，则遍历每一个bb，使得bb的Input为Control flow的约束，Output为Transfer function的约束。

Sample

这里举例说明，存在如下的CFG。

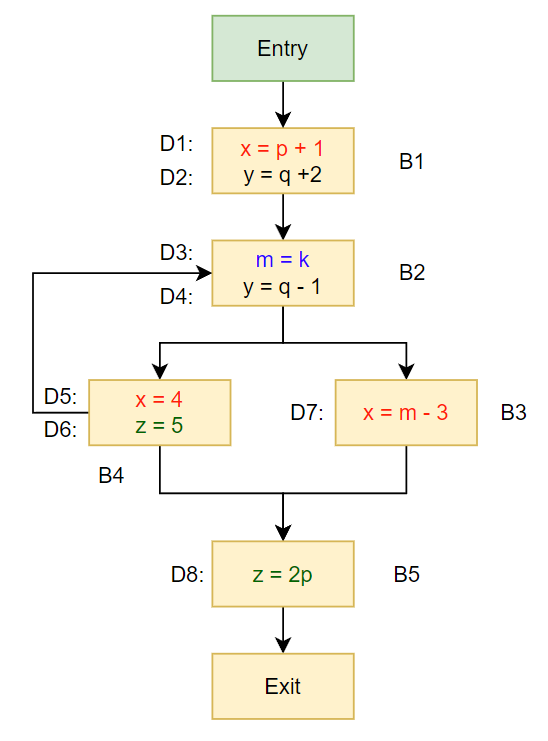
这里将对不同变量的定义用颜色区分，可以看到，每一个statement都对应一个D的定义操作。

这样的CFG可以有下面的代码转化而来：

D1
D2
do{
	D3
	D4
	if(...){
		D5
		D6
	}
	else{
		D7
		break
	}
} while(...)
D8

这里将八个Statement，即八个定义操作抽象为bit。0：表示到该点不能reach，1：到该点可以reach；

1st-traverse

根据算法，初始化后，所有的Output为空。

进入Entry，没有变量的定义，都不能reach

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

1-Entry \ 0 0 0 0 0 0 0 0
进入第一个Basic Block，B1有两个statement，分别是D1和D2，通过$OUT[B] = gen_B \space ∪ \space (IN[B] - kill_B)$可以得到：
- $gen_{B_1}$ = {D1,D2}，$kill_{B_1}$ = {D4,D5,D7}
因此，在执行了B1的statement后，有：

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

2-B1 D1: x = p + 1
D2: y = q + 2 1 1 0 0 0 0 0 0
进入B2后，根据$IN[B]=∪_{P \space a\space predecessor\space of\space B}OUT[P]$，找到B2的前驱，一共有两个，分别是B1和B4。B1的OUT[B1]=11000000，B4的OUT[B4]=00000000，两者做或操作，作为IN[B2]，因此IN[B2]=11000000；

在B2的statement中，存在：1. 引入新变量m；2.对y变量的再次定义，因此有：
- $gen_{B_2}$ = {D3,D4}，$kill_{B_2}$ = {D2}
因此将进行kill，而D2目前为1，kill掉后为0；

因此B2的OUT[B2]=10110000，这同时也是B3、B4的IN；

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

3-B2 D3: m = k
D4: y = q - 1 1 0 1 1 0 0 0 0
由于B2有两个分支，这里按顺序先考虑B3；

B3对变量x进行了重定义，有：
- $gen_{B_3}$ = {D7}，$kill_{B_3}$ = {D1,D5}
因此对于IN[B3]=10110000，将有OUT[B5]=00110010

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

4-B3 D7: x = m - 3 0 0 1 1 0 0 1 0
对于B4，同样的有：
- $gen_{B_4}$ = {D5,D6}，$kill_{B_4}$ = {D1,D7,D8}
IN[B4]=10110000，将有OUT[B5]=00111100；

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

5-B4 D5: x = 4
D6: z = 5 0 0 1 1 1 1 0 0
对于B5，根据$IN[B]=∪_{P \space a\space predecessor\space of\space B}OUT[P]$，找到其对应的前驱，OUT[B3]、OUT[B4]，进行或操作，得到IN[B5]=00111110;

同样有：
- $gen_{B_5}$ = {D8}，$kill_{B_5}$ = {D6}
对于IN[B5]=00111110，有OUT[B5]=00111011；

Step Statement D1 D2 D3 D4 D5 D6 D7 D8

6-B5 D8: z = 2p 0 0 1 1 1 0 1 1

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
1-Entry	\	0	0	0	0	0	0	0	0

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
2-B1	D1: x = p + 1 D2: y = q + 2	1	1	0	0	0	0	0	0

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
3-B2	D3: m = k D4: y = q - 1	1	0	1	1	0	0	0	0

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
4-B3	D7: x = m - 3	0	0	1	1	0	0	1	0

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
5-B4	D5: x = 4 D6: z = 5	0	0	1	1	1	1	0	0

Step	Statement	D1	D2	D3	D4	D5	D6	D7	D8
6-B5	D8: z = 2p	0	0	1	1	1	0	1	1

进入Exit，完成第一次遍历，是否需要再次进行循环的条件是while(changes to any OUT occur)，显然出现了新的OUT，所以仍然需要进行遍历。

Changes occur in OUT[] of B1,B2,B3,B4,B5

这里对每一个Basic Block的情况进行汇总：

BB	IN[]	Statement	$gen_B$	$kill_B$	D1	D2	D3	D4	D5	D6	D7	D8
B1	Entry	D1: x = p + 1 D2: y = q + 2	{D1,D2}	{D4,D5,D7}	1	1	0	0	0	0	0	0
B2	B1、B4	D3: m = k D4: y = q - 1	{D3,D4}	{D2}	1	0	1	1	0	0	0	0
B3	B2	D7: x = m - 3	{D7}	{D1,D5}	0	0	1	1	0	0	1	0
B4	B2	D5: x = 4 D6: z = 5	{D5,D6}	{D1,D7,D8}	0	0	1	1	1	1	0	0
B5	B3、B4	D8: z = 2p	{D8}	{D6}	0	0	1	1	1	0	1	1

2nd-traverse

在第二次遍历时，

对于B1，OUT是不需要重新计算的；
而对于B2而言，其IN分别来自B1、B4，要对他们的IN进行或运算，即IN[B1]=11000000、IN[B4]=00111100，可以得到IN[B2]=11111100，在根据$gen_B$、$kill_B$进行操作后，得到OUT[B2]=10111100；
对于B3，其IN为B2的OUT，所以IN[B3]=10111100，OUT[B3]=00110110；
对于B4，其IN为B2的OUT，所以IN[B4]=10111100，OUT[B4]=00111100；
对于B5，其IN为B3、B4的OUT，所以IN[B5]=00111110，OUT[B5]=00111011

进入Exit，完成第二次遍历后，检查OUT判断是否要进行第三次循环；

BB	IN[]	Statement	$gen_B$	$kill_B$	D1	D2	D3	D4	D5	D6	D7	D8
B1	Entry	D1: x = p + 1 D2: y = q + 2	{D1,D2}	{D4,D5,D7}	1	1	0	0	0	0	0	0
B2	B1、B4	D3: m = k D4: y = q - 1	{D3,D4}	{D2}	1	0	1	1	1	1	0	0
B3	B2	D7: x = m - 3	{D7}	{D1,D5}	0	0	1	1	0	1	1	0
B4	B2	D5: x = 4 D6: z = 5	{D5,D6}	{D1,D7,D8}	0	0	1	1	1	1	0	0
B5	B3、B4	D8: z = 2p	{D8}	{D6}	0	0	1	1	1	0	1	1

可以看到Changes occur in OUT[] of B2,B3，因此需要进行第三次遍历；

3rd-traverse

遍历结束后，OUT没有变化，因此不需要进行第四次遍历。

Why this algorithm can finally stop?

Transfer Function:
$$
OUT[B] = gen_B \space ∪ \space (IN[B] - kill_B)
$$

$gen_B$ and $kill_B$ remain unchanged
When more facts flow in IN[B], the “more facts” either
- is killed, or
- flows to OUT[B]（$survivor_B$）
When a fact is added to OUT[B], through either $gen_B$, or $survivor_B$, it stays there forever
Thus OUt[B] newver shrinks (e.g., 0->1, or 1->1)
As the set of facts is finite (e.g., all definitions in the program), there must exist a pass of iteration during which nothing is added to any OUT, and then the algorithm terminates

Safe to terminate by condition do…while?

迭代和Transfer Function的原因，最终算法会到达一个不动点，这个不动点是一个safe-approximation的结果。

assumption

对于一个Basic Block，同样的输入会得到同样的输出，即对于输入x，res = $gen_B\space ∪\space x\space -\space kill_B$ ，x不变时，res也不会变。
对于B1，不需要重复计算IN[B1]和OUT[B1]。
对于每个Basic Block的OUT中，D如果为1，则表示该定义能够reach到当前BB，否知则否。
In each data-flow analysis application, we associate with every program point a data-flow value taht represents an abstraction of the set of all possible program states that can be observed for that point. Data-flow analysis is to find a solution to a set of safe-approximation-directed constraints on the IN[s]'s and OUT[s]'s, for all statements s.
- constraints based on semantics of statements(transfer funcitons)
- constraints based on the flows of control

Live Variables Analysis

Preliminary

Live variables analysis tells whether the value of variable v at program point p could be used along some path in CFG starting at p. If so, v is live at p; otherwise, v is dead at p.

v§ == should not be redefined before usage => use(v)

Information of live variables can be used for register allocations.e.g., at some point all registers are full and we need to use one, then we should favor using a register with a dead value. - 如果存放变量的寄存器都被占用了，那么应该首先使用存放dead value的寄存器来存放新的value。

Understanding

Data Flow Values/Facts - Abstraction
- All the variables in a program
- Can be represented by bit vectors
  
  e.g., v1,v2,v3,…,v100 -> 100 bits

Safe-approximation

Transfer Function

由：
$$
OUT[B]=∪_{S \space a\space successor\space of\space B}\space IN[B]
$$

得到：
$$
IN[B]=use_B\space ∪\space (OUT[B]-def_B)
$$
对Transfer Function的理解：

采取何种分析方式？Backward or Forward？
已知OUT[B]，何来IN[B]？

对于下面的例子：

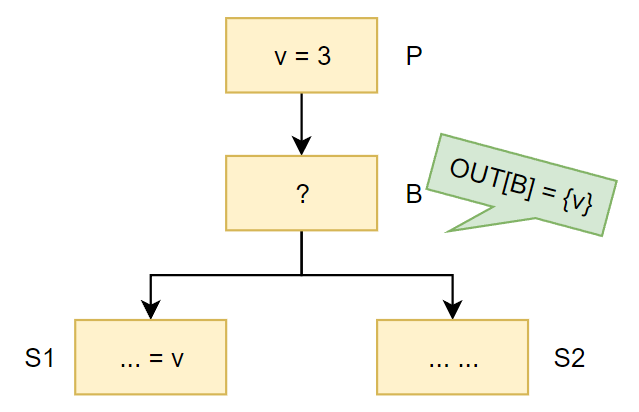
在已知OUT[B]={v}的情况下，如何去推算IN[B]呢？

这里先举几个例子，针对不同的?，有以下内容形成的表格：

?	$use_B$	$def_B$	IsBefore Flag	IN[B]	Explanation
k = n	{n}	{k}	0	{v}	not used, not redefined
k = v	{v}	{k}	0	{v}	used
v = 2	{}	{v}	0	{}	not used, redefined
v = v - 1	{v}	{v}	1	{v}	used before redefined
v = 2 k = v	{v}	{v, k}	0	{}	redefined before used
k = v v = 2	{v}	{k, v}	1	{v}	used before redefined

在redefine之前如果use，那么认为该变量仍然是live的。

可以看到，其实很多数据流分析的pattern都是$gen_B$和$kill_B$的结构；

因此，对于$IN[B]$的推算，由$OUT[B]-def_B$可以去掉那些重定义的value，但是如果在重定义前使用了这些变量，则需要加回来$use_B$，由此才得到$IN[B]$

Algorithm

INPUT：CFG(def_B and useB computed for each basic block B)
OUTPUT：IN[B] and OUT[B] for each basic block B
Method：

Sample

有如下例子：

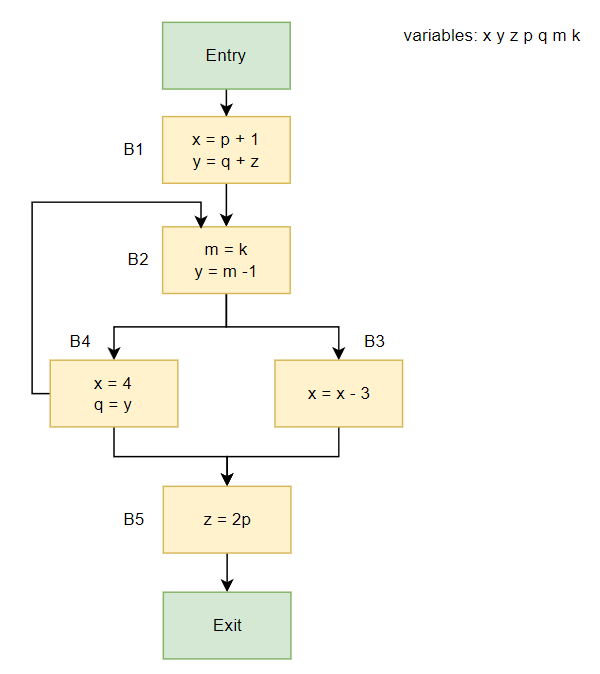
首先进行初始化，将所有OUT[B]、IN[B]标记为0000000；

x y z p q m k

0 0 0 0 0 0 0
根据Backward和transfer function($IN[B]=use_B\space ∪\space (OUT[B]-def_B)$)进行推算；

简单理解就是，对于$def_B$进行kill操作（标0），对于$use_B$进行gen操作（标1）；
- 对于B5而言，有：
  
  $use_B$={p}, $def_B$={z}, $OUT[B]={0000000}$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B5 z = 2p 000 0000 {p} {z} 0 1 000 1000
- 对于B4而言，B4有两个后继{B5, B2}，其$OUT[B4]$为$IN[B2]$和$IN[B5]$的Union，有：
  
  $use_B$={y}, $def_B$={x, q}, $OUT[B4]=0000000 ∪ 0001000 = 0001000$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B4 x = 4
  q = y 000 1000 {y} {x, q} 0 1 0 010 1000
- 对于B3而言，有：
  
  $use_B$={x}, $def_B$={x}, $OUT[B3]=0001000$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B3 x = x - 3 000 1000 {x} {x} 0 1 0 100 1000
- 对于B2而言，B2有两个后继，为{B3, B4}，因此其$OUT_[B2]$为$IN[B3]$和$IN[B4]$的Union，有：
  
  $use_B$={k, m}, $def_B$={m, y}, $OUT[B2]=1101000$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B2 m = k
  y = m - 1 110 1000 {k, m} {m, y} 0 0 1 100 1001
- 对于B1而言，有：
  
  $use_B$={p, q, z}, $def_B$={x, y}, $OUT[B1]=1001001$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B1 x = p + 1
  y = q + z 100 1001 {p, q, z} {x, y} 0 0 1 1 1 001 1101
由此第一次推算结束了。

那么是否需要进行第二次的推算呢？判断条件是changes to any IN[B] occur，所以仍然需要进行循环推算；
第二次推算继续：

根据推算规则：
$$
IN[B]=use_B\space ∪\space (OUT[B]-def_B)
$$
对于每一个Basic Block，其中的Statment都是不变的，意味着$use_B$和$def_B$是不变的，因此当$OUT[B]$不变时，$IN[B]$也不会变；
- 对于B5而言，依然不变：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B5 z = 2p 000 0000 {p} {z} 0 1 000 1000
- 对于B3而言，由于$IN[B5]$不变，其前驱的Basic Block如若只有一个后继，那么该Basic Block的IN[B]不变，意味着B3的$OUT[B]$也不会变。
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B3 x = x - 3 000 1000 {x} {x} 0 1 0 100 1000
- 对于B4而言，其有两个后继B2、B5，根据规则有：
  
  $use_B$={y}, $def_B$={x, q}, $OUT[B4]=1001001 ∪ 0001000 = 1001001$
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B4 x = 4
  q = y 100 1001 {y} {x, q} 0 1 0 010 1001
- 对于B2而言，B2有两个后继，为{B3, B4}，因此其$OUT_[B2]$为$IN[B3]$和$IN[B4]$的Union，有：
  
  $use_B$={k, m}, $def_B$={m, y}, $OUT[B2]=1101001$
  
  得到：
  
  Basic Block Statement $OUT[B_i]$ $use_B$ $def_B$ x y z p q m k $IN[B_i]$
  
  B2 m = k
  y = m - 1 110 1001 {k, m} {m, y} 0 0 1 100 1001
- 对于B1而言，$IN[B2]$没有变化，意味着$OUT[B1]$没有变化，因此$IN[B1]$不变；
对于本次遍历而言，变化的$IN[B]$有$IN[B4]$，因此还需要进行第三次的循环遍历；
根据规则，只有$IN[B4]$，即只有$OUT[B2]$发生变化，根据上一次遍历中对$IN[B2]$的推算没有变化，因此这次遍历不会产生IN[B]的变化，由此循环结束；得到的Final analysis result为对于每个Basic Block，其IN[B]中对应变量标记如果为1，则代表在进入当前Basic Block前，该变量为live；

x	y	z	p	q	m	k
0	0	0	0	0	0	0

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B5	z = 2p	000 0000	{p}	{z}			0	1				000 1000

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B4	x = 4 q = y	000 1000	{y}	{x, q}	0	1			0			010 1000

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B3	x = x - 3	000 1000	{x}	{x}	0	1			0			100 1000

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B2	m = k y = m - 1	110 1000	{k, m}	{m, y}		0				0	1	100 1001

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B1	x = p + 1 y = q + z	100 1001	{p, q, z}	{x, y}	0	0	1	1	1			001 1101

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B5	z = 2p	000 0000	{p}	{z}			0	1				000 1000

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B3	x = x - 3	000 1000	{x}	{x}	0	1			0			100 1000

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B4	x = 4 q = y	100 1001	{y}	{x, q}	0	1			0			010 1001

Basic Block	Statement	$OUT[B_i]$	$use_B$	$def_B$	x	y	z	p	q	m	k	$IN[B_i]$
B2	m = k y = m - 1	110 1001	{k, m}	{m, y}		0				0	1	100 1001

Available Expressions Analysis

Must Analysis

Preliminary

An expreesion $x \space op \space y$ is available at program point p if (1) all paths from the entry to p must pass through the evaluation of $x \space op \space y$, and (2) after the last evaluation of $x \space op \space y$, there is no redefinitoin of x or y.

This definitoin means at program p, we can replace expression x op y by the result of its last evaluation
The information of available expressions can be used for detecting global common subexpressions.

Undestanding

Abstraction:

Data Flow Values/Facts
- All the expressions in a program
- Can be represented by bit vectors

Safe-approximation

Forward?
A sample =>
- Add to OUt the expression x op y(gen)
- Delete from IN any expression involving variable a(kill)
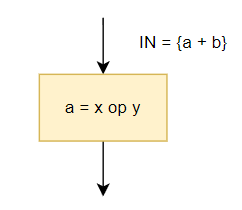
Transfer Function:
$$
OUT[B]=gen_B \space ∪ \space (IN[B]-kill_B)
$$

$$
IN[B]=∩_{P \space a \space predecessor \space of \space B}OUT[P]
$$

由于must analysis，需要对IN[B]采取$∩$的方法；

对于：
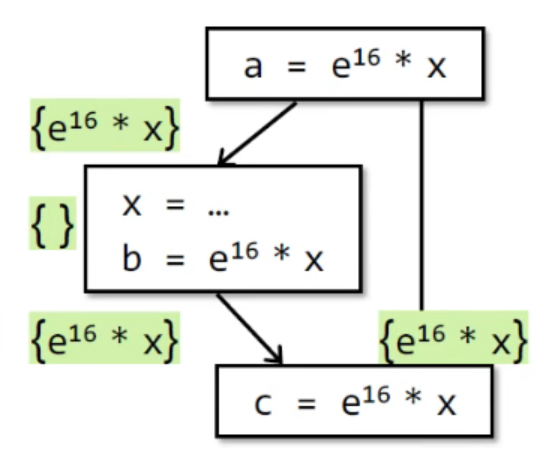
1. 在$a=e^{{16}*x$后，$OUT[B]$={$e}{16}*x$}；
2. 在经过对x的赋值后，由于对x的引用，OUT[B]被置空，但是在对b的定义中使用了$b=e^{16}*x$后，重新gen；
3. 最终在$c=e^{16}*x$的Basic Block前，IN[B]为{$e^{16}*x$}；
有一个问题就是，其中x的值发生了变化，如何避免这种错误发生呢？如果将a, b, c都替换成t，这样一来从a->c的两个分支，无论走哪个分支，如果t的值被覆盖，也能由自身继承，因此达到了must的效果；

Algorithm

Sample

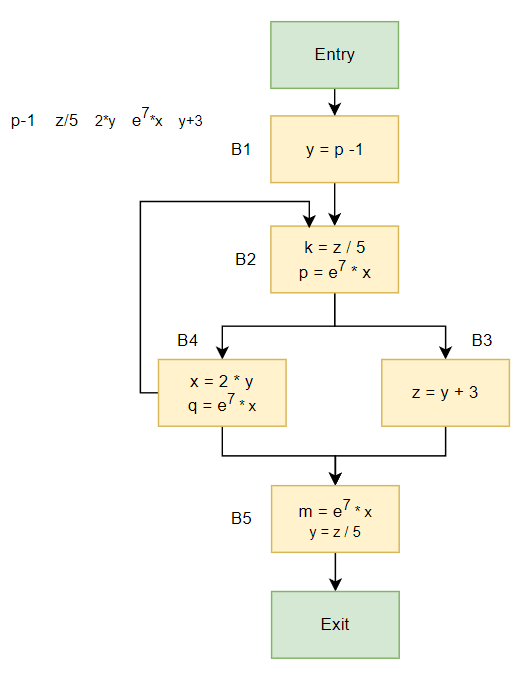
对于如上的例子，进行分析：

首先初始化，将所有basic block的OUT[B]设置为11111， entry设置为00000；
开始循环
- 对于B1而言，有：
  
  $gen_B$={$p-1$}, $kill_B$={y}, IN[B]=00000
  
  得到：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B1 00000 {$p-1$} {y} 1 0 0 10000
- 对于B2而言，IN[B2] = 11111 ∩ 10000 = 10000，有：
  
  $gen_B$={$z/5$, $e^7*x$}, $kill_B$={k, p}
  
  得到：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B2 10000 {$z/5$, $e^7*x$} {k, p} 0 1 1 01010
- 对于B3而言，有：
  
  $gen_B$={$y+3$}, $kill_B$={z}, IN[B]=01010
  
  得到：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B3 01010 {$y+3$} {z} 0 1 00011
- 对于B4而言，有：
  
  $gen_B$={$2y$, $e^7x$}, $kill_B$={x, q}, IN[B]=01010
  
  得到：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B4 01010 {$2y$, $e^7x$} {x, q} 1 1 01110
- 对于B5而言，有：
  
  $gen_B$={$e^7*x$, $z/5$}, $kill_B$={m, y}, IN[B] = 01110 ∩ 00011 = 00010
  
  得到：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B5 00010 {$e^7*x$, $z/5$} {m, y} 1 0 1 0 01010
由于OUT[B]发生了变化，再次进入循环；
- 对于B1而言，由于IN[B]不变，所以OUT[B]没变；
- 对于B2而言，由于IN[B2] = 10000 ∩ 01110 = 00000，有：
  
  Basic Block $IN[B_i]$ $gen_B$ $kill_B$ $p-1$ $z/5$ $2*y$ $e^7*x$ $y+3$ $OUT[B_i]$
  
  B2 00000 {$z/5$, $e^7*x$} {k, p} 0 1 1 01010
  
  结果没变；
- 对于B3而言，IN[B]没变，所以OUT[B]没变；
- 对于B4而言，IN[B]没变，所以OUT[B]没变；
- 对于B5而言，IN[B]= 00011 ∩ 01110 = 00010，没变，所以OUT[B]没变；
由于OUT[B]没有发生变化，因此循环结束；

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B1	00000	{$p-1$}	{y}	1		0		0	10000

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B2	10000	{$z/5$, $e^7*x$}	{k, p}	0	1		1		01010

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B3	01010	{$y+3$}	{z}		0			1	00011

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B4	01010	{$2y$, $e^7x$}	{x, q}			1	1		01110

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B5	00010	{$e^7*x$, $z/5$}	{m, y}		1	0	1	0	01010

Basic Block	$IN[B_i]$	$gen_B$	$kill_B$	$p-1$	$z/5$	$2*y$	$e^7*x$	$y+3$	$OUT[B_i]$
B2	00000	{$z/5$, $e^7*x$}	{k, p}	0	1		1		01010

Analysis Comparison

	Reaching Definitions	Live Variables	Available Expressions
Domain	definition(set of definitions)	value(set of variables)	x op y(set of expressions)
Direction	Forward	Backward	Forward
May/Must	May	May	Must
Boundary	entry.out(OUT[entry]=∅)	exit.in(IN[exit]=∅)	entry.out(OUT[entry]=∅)
Initialization	OUT => 0(OUT[B]=∅)	IN => 0(IN[B]=∅)	OUT => 1(OUT[B]=∪)
Transfer Function	$OUT[B]=gen_B+(IN[B]-kill_B)$ $IN[B]=∪_{P \space a\space predecessor\space of\space B}OUT[P]$	$IN[B]=use_B+(OUT[B]-def_B)$ $OUT[B]=∪_{P \space a\space predecessor\space of\space B}IN[P]$	$OUT[B]=gen_B+(IN[B]-kill_B)$ $IN[B]=∩_{P \space a\space predecessor\space of\space B}OUT[P]$
Meet	OUT not change(∪)	IN not change(∪)	OUt not change(∩)

Summary

Overview of Data Flow Analysis
Preliminaries of Data Flow Analysis
Three kinds of Analysis
- Reaching Definitions Analysis
- Live Variables Analysis
- Available Expressions Analysis
Key Point
- Understand the three data flow analysis
- Can tell the differences and similarities of the three data flow analyses(the front form)
- Understand the iterative algorithm and can tell why it is able to terminate(OUT&IN,why the progess can stop?)

static_program_analysis_03-data_flow_analysis

Data Flow Analysis

Overview of Data Flow Analysis

What is Data Flow Analysis

Preliminaries of Data Flow Analysis

Input & Output States

Nations for Transfer Function’s Constraints

Notations for Control Flow’s Constraints

Data Flow Analysis Applications

Issues Not Covered

Reaching Definitions Analysis

Preliminary

Understanding

Algorithm

Sample

1st-traverse

2nd-traverse

3rd-traverse

Why this algorithm can finally stop?

Safe to terminate by condition do…while?

assumption

Live Variables Analysis

Preliminary

Understanding

Algorithm

Sample

Available Expressions Analysis

Preliminary

Undestanding

Algorithm

Sample

Analysis Comparison

Summary