绪论

这一章粗略过一下，讲一下重点即可。

知识框架图

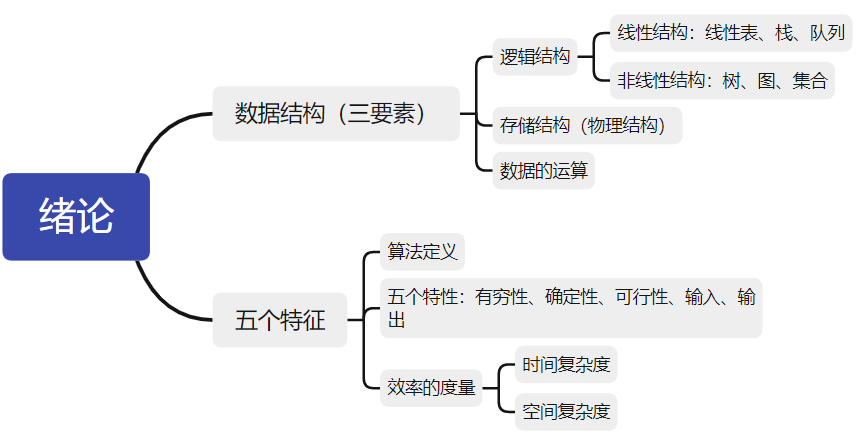
数据结构的一些概念

【数据】- 信息载体；

【数据项】- 构成数据元素的不可分割的最小单位；

【数据元素】- 数据的基本单位，可由若干数据项组成；

【数据对象】- 具有相同性质的数据元素的集合，是数据的子集；

【数据类型】- 一个值的集合和定义在此集合上的一组操作的总称，包括类型有：1.原子类型 2.结构类型 3.抽象数据类型

【数据结构】- 相互之间存在一种或多种特定关系的数据元素的集合。在任何问题中，数据元素都不是孤立存在的，它们之间存在某种关系，这种数据元素相互之间的关系称为结构(structure)。数据结构包括三方面的内容：1.逻辑结构 2.存储结构 3.数据的运算。

数据的逻辑结构和存储结构是密不可分的，一个算法的设计取决于所选定的逻辑结构，而算法的实现依赖于所采用的存储结构

数据结构三要素

上面提到了数据结构的三要素，分别是：

逻辑结构
存储结构
数据的运算

逻辑结构

数据元素之间的逻辑关系，从逻辑关系上描述数据。它与数据的存储无关，是独立于计算机的。

逻辑结构分为线性结构和非线性结构。

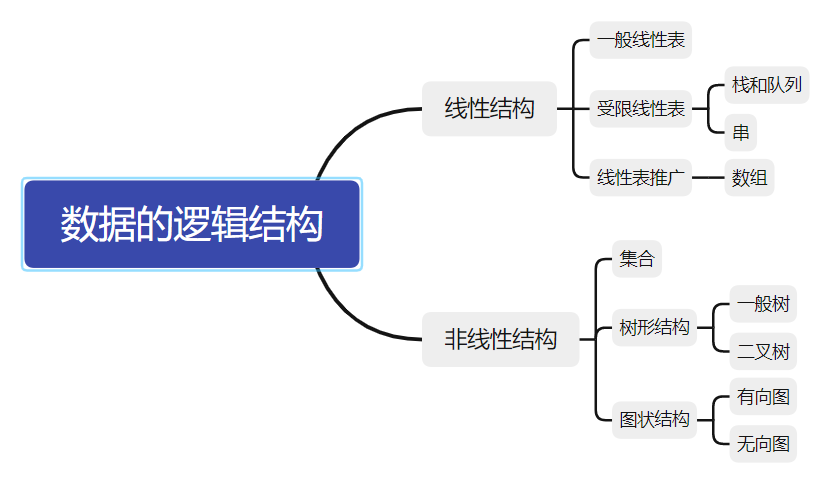
存储结构

存储结构是数据结构在计算机中的表示（映像），也称为物理结构。其包括数据元素的表示和关系的表示。存储方式主要有：

顺序存储：把逻辑上相邻的元素存储在物理位置相邻的存储单元中，元素之间的关系由存储单元的邻接关系来体现。
- 优点：可以实现随机存取，每个元素占用最少的存储空间；
- 缺点：只能使用相邻的一整块存储单元，可能产生较多外部碎片；
链式存储：逻辑相邻的元素在物理位置上不需要相邻，借助指示元素存储地址的指针来表示元素之间的逻辑关系。
- 优点：不会出现碎片，充分利用了所有存储单元；
- 缺点：每个元素因存储指针而占用额外的存储空间，而且只能实现顺序存取；
索引存储：在存储元素信息的同时，建立附加的索引表，索引表的每一项称为索引项，一般形式是（关键字，地址）。
- 优点：检索速度快；
- 缺点：附加的索引表占用而外空间，增加和删除也需要修改索引；
散列存储：根据元素的关键字直接计算处该元素的存储地址，哈希(Hash)存储。
- 优点：检索、增加和删除结点操作都很快；
- 缺点：如果散列函数较差，可能出现元素存储单元冲突；

数据的运算

包括：

运算的定义：针对逻辑结构，说明运算的功能；
运算的实现：针对存储结构，指出运算的具体操作步骤；

算法和算法评价

基本概念

五个重要性：

有穷性
确定性
可行性
输入
输出

好的算法还要考虑以下目标：

正确性
可读性
健壮性
效率与低存储量需求

算法效率的度量

时间复杂度
空间复杂度

时间复杂度

一个语句的频度指的是该语句在算法中被重复执行的次数。

算法中所有语句的频度之和记为 $T{(n)}$ ，它是该算法问题规模 $n$ 的函数。

时间复杂度主要分析 $T{(n)}$ 的数量级。基本运算的频度 $f{(n)}$（最深层循环内的语句的频度）与 $T{(n)}$ 有相同数量级。取 $f{(n)}$ 中随 $n$ 增长最快的项，将其系数置为 $1$ 作为时间复杂度的度量。例如， $f{(n)}=an^3+bn2+cn$ 的复杂度为$O{(n^3)}$ 。

记为：
$$
T{(n)}=O(f{(n)})
$$
$O$ 的含义是 $T(n)$ 的数量级，严格的数学定义是：若 $T(n)$ 和 $f(n)$ 是定义在正整数集合上的两个函数，则存在正常数 $C$ 和 $n_{0}$，使得当 $n \geq n_0$ 时，都满足 $0 \leq T(n) \leq Cf(n)$。

时间复杂度还取决于输入数据的性质，如：

对于数组arr[0...n-1]，查找给定值k的算法大致为：

i=n-1;
while(i>=0&&(arr[i]!=k))
	i--;
return i;

存在两种情况：

若arr中没有等于k的元素，则语句i--;的频度是 $f(n)=n$ ；
若arr中最后一个元素就等于k，则语句i--;的频度是 $0$ ;

一般总是考虑在最坏情况下的时间复杂度，以保证算法的运行时间不会比之更长。

在分析一个程序的时间复杂度时，有以下两个规则：

加法规则
$$
T(n)=T_1(n)+T_2(n)=O(f(n))+O(g(n))=O(max(f(n),g(n)))
$$

即：当两个频度的语句处于同一层时，该层的时间复杂度等于频度更大的语句的频度。
乘法规则
$$
T(n)=T_1(n) \times T_2(n)=O(f(n)) \times O(g(n))=O(f(n) \times g(n))
$$
即：当两个频度的语句进行嵌套时，其整体的时间复杂度等于嵌套各层的语句频度相乘。

时间复杂度比较

$O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(n3)<O(2^n)<O(n!)<O(nn)$

空间复杂度

$S(n)$ 定义为该算法所耗费的存储空间，是问题规模 $n$ 的函数，记为：
$$
S(n)=O(g(n))
$$
一个程序在执行时除需要存储空间来存放本身所用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为实现计算所需信息的辅助空间。若输入数据所占空间只取决于问题本身，和算法无关，则只需分析除输入和程序之外的额外空间。

算法原地工作指的是算法所需的辅助空间为常量，即 $O(1)$ 。

归纳总结

分析程序的时间复杂度是重点。

循环主题中的变量参与循环条件的判断

此类型的题目应该找出主体语句中于 $T(n)$ 成正比的循环变量，将之代入条件中进行计算。例如：
// sample 1
int i=1;
while(i<=n)
i=i*2
在这个例子中，i*2 的次数正是主体语句执行次数 $t$ ，因此执行 $t$ 次后，有 $2^t \leq n$ ，取对数后可以得到 $t \leq log_2n$ ，即为 $T(n)=O(log_2n)$ 。

又例如：
// sample 2
int y=5;
while((y+1)*(y+1)<n)
y=y+1;
在这个例子中，y+1 的次数恰好与 $T(n)$ 成正比。

记 $t$ 为该程序执行次数。
1. 执行 $t$ 次后，先计算循环体里的语句：
  $$
  y=y_0+t=5+t
  $$

然后将 $y$ 代入循环条件得到：
$$
(t+5+1) \times (t+5+1) < n
$$
即为：
$$
t<\sqrt n -6
$$
即 $T(n)=O(\sqrt n)$

循环主题中的变量不参与循环条件的判断

采用 数学归纳法 或 直接累计循环次数。

多层循环时，从内到外分析，忽略单步语句、条件判断语句，只关注主体语句的执行次数。

又可分为递归程序和非递归程序：
- 递归程序是用公式递推，例子如下：
  int fact(int n){
  if(n<=1)
  return 1;
  return n * fact(n-1);
  }
  递推为：
  
  $$
  \begin{equation*}
  \begin{split}
  T(n)
  & =1+T(n-1)\
  & =1+1+T(n-2)\
  & =\space …\
  & =n-1+T(1)\
  & =n
  \end{split}
  \end{equation*}
  $$
  最终可以得到 $T(n)=O(n)$
- 非递归程序可以直接累计次数。