data_structure_02_linear_list
线性表
重点内容:
- 线性表的定义和基本操作
- 线性表的实现:顺序存储、链式存储、线性表的应用
知识框架:
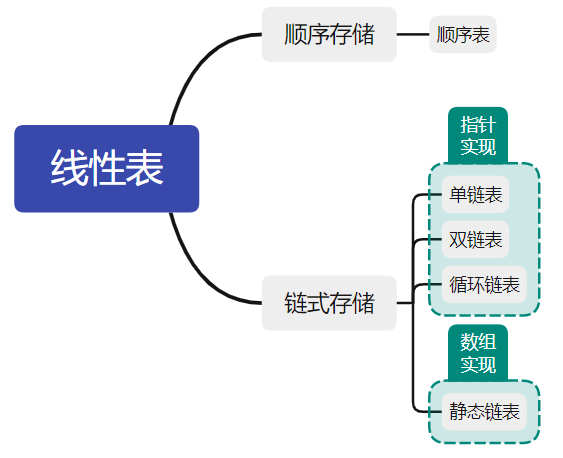
线性表的定义和基本操作
线性表的定义
线性表是具有相同数据类型的 $n \space (n \geq 0)$ 个数据元素的有限序列,其中 $n$ 为表长,为0是代表线性表为空表。若用 $L$ 命名线性表,则一般表示为:
$$
L=(a_1,a_2,…,a_i,a_{i+1},…,a_n)
$$
线性表逻辑特性为:
- $a_1$ 为唯一的”第一个“数据元素,又称为表头元素 ;
- $a_n$ 是唯一的”最后一个“数据元素,又称为表尾元素;
- 除第一个元素外,每个元素有且仅有一个直接前驱;
- 除最后一个元素外,每个元素有且仅有一个直接后继;
注意:
- 线性表是一种逻辑结构,表示元素之间一对一的相邻关系;
- 顺序表和链表强调的是存储结构,和线性表属于不同层面的概念;
线性表的基本操作
线性表的主要操作有:
InitList(&L)- 初始化表,构造一个空的线性表Length(L)- 求表长,返回线性表L的长度,即其中元素的个数LocateElem(L, e)- 按值查找操作,在表L中查找具有给定值的元素GetElem(L, i)- 按位查找操作,获取表L中第i个位置的元素的值ListInsert(&L, i, e)- 插入操作,在表L中第i个位置插入指定元素eListDelete(&L, i, &e)- 删除操作,删除表L中第i个位置的元素,并用e返回删除元素的值PrintList(L)- 打印线性表,按前后顺序输出线性表L的所有元素值Empty(L)- 判空操作,若L为空表,则返回true,否则返回falseDestroyList(&L)- 销毁操作,销毁线性表,释放L所占用的内存空间
注意:
- 基本操作的实现取决于存储结构
&表示C++中表示引用调用,在C语言中采用指针可达到同样的效果
线性表的顺序表示
顺序表的定义
线性表的顺序存储称为顺序表。
是用一组地址连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理位置上也相邻。即逻辑顺序与物理顺序相同。
线性表的顺序存储结构是一种随机存储的存储结构。典型的就是高级程序设计语言中的数组。但是要注意的是,线性表元素的位序从1开始,而数组的元素下标从0开始。
// 静态分配 |
顺序表的特点有:
- 随机访问,通过首地址和元素序号可以在 $O(1)$ 的时间内找到指定元素;
- 存储密度高,每个结点只存储数据元素;
- 逻辑相邻的元素物理相邻,插入和删除操作需要移动大量元素;
顺序表上的操作
- 插入
- 删除
- 按值查找
以下列顺序表结构为例:
|
插入
/* 按位插入指定数值 */ |
对于插入操作而言:
-
最好情况:在表尾(位序为
L.length+1,下标为L.length)插入,不移动元素 -
最坏情况:在表头(位序为1,下标为0),需要移动
L.length次 -
平均情况:假设 $p_i \space (p_i=\frac{1}{n+1})$ 是在第 $i$ (这里的 $i$ 是位序)个位置上插入一个结点的概率,则在长度为 $n$ 的线性表中插入一个结点时,$n-i+1$ 为需要挪动的次数,则所需要移动结点的平均次数为:
$$
\begin{equation}
\begin{split}
N
&=\sum_{i=1}^{n+1}p_i(n-i+1)\
&=\sum_{i=1}^{n+1}\frac{1}{n+1}(n-i+1)\
&=\frac{1}{n+1}\sum_{i=1}^{n+1}(n-i+1)\
&=\frac{1}{n+1} \times \frac{n(n+1)}{2}\
&=\frac{n}{2}
\end{split}
\end{equation}
$$
即插入算法的平均时间复杂度为 $O(n)$ 。
删除
/* 删除指定位序的元素,并用变量 del_e 返回 */ |
对于删除操作而言:
-
最好情况:删除表尾(位序为
L.length,下标为L.length-1)元素,不移动元素 -
最坏情况:删除表头(位序为1,下标为0),需要移动
L.length-1次 -
平均情况:假设 $p_i \space (p_i=\frac{1}{n})$ 是删除第 $i$ (这里的 $i$ 是位序)个位置的结点的概率,则在长度为 $n$ 的线性表中删除一个结点时,$n-i$ 为需要挪动的次数,则所需要移动结点的平均次数为:
$$
\begin{equation}
\begin{split}
N
&=\sum_{i=1}^{n}p_i(n-i)\
&=\sum_{i=1}^{n}\frac{1}{n}(n-i)\
&=\frac{1}{n}\sum_{i=1}^{n}(n-i)\
&=\frac{1}{n} \times \frac{n(n-1)}{2}\
&=\frac{n-1}{2}
\end{split}
\end{equation}
$$
即删除算法的平均时间复杂度为 $O(n)$ 。
按值查找
/* 按值查找位序 */ |
对于按值查找操作而言:
-
最好情况:查找的元素在表头,只需要执行条件语句一次,时间复杂度为 $O(1)$
-
最坏情况:查找的元素在表尾或不存在,需要执行条件语句
L.length次,即 $n$ 次,时间复杂度为 $O(n)$ -
平均情况:假设 $p_i \space (p_i=\frac{1}{n})$ 是查找的元素在第 $i$ (这里的 $i$ 是位序)个位置的结点的概率,则在长度为 $n$ 的线性表中查找值为
element的结点时,所需要执行条件语句的平均次数为:
$$
\begin{equation}
\begin{split}
N
&=\sum_{i=1}^{n}p_i \times i\
&=\sum_{i=1}^{n}\frac{1}{n} \times i\
&=\frac{1}{n}\sum_{i=1}^{n}i\
&=\frac{1}{n} \times \frac{n(n+1)}{2}\
&=\frac{n+1}{2}
\end{split}
\end{equation}
$$
即线性表按值查找算法的平均时间复杂度为 $O(n)$ 。
课后题
|
线性表的链式表示
链式存储线性表时,不需要使用地址连续的存储单元,不要求逻辑上相邻的元素在物理位置上也相邻,通过“链”建立其数据元素之间的逻辑关系,插入和删除操作只需要修改指针,但是也会失去随机存储的优点。
单链表的定义
线性表的链式存储又称为单链表,通过一组任意的存储单元来存储线性表中的数据单元,为了建立元素间的线性关系,对每个链表结点,除了存放元素自身的信息外,还存放一个指向其后继的指针。
typedef struct LNode |
需要注意的是:
- 非随机存取的存储结构,不能直接找到表中某个特定结点,查找特定结点需要从表头开始遍历。
- 通常用头指针来标识一个单链表,头指针为NULL时表示一个空表。
- 在第一个结点之前通常附加一个头结点,数据域可以为NULL也可以是表长,其指针指向第一个元素。带头结点的优点:
- 第一个元素结点的操作和表上其他位置的结点操作一致
- 无论链表是否为空,头指针都指向头结点的非空指针(空表中头结点的指针域为空)
单链表上的操作
按顺序插入结点
-
头插法
LinkList InsertListFromHead(LinkList &L, int n)
{
/* 创建头结点,并使其 next 指向 NULL */
L = (LinkList)malloc(sizeof(LNode)); /* 注意这里不是 LinkList *,因为在struct的定义里已经被设置为了数组形式存储LNode */
L->next = NULL;
/* 创建要插入结点 */
for (int i = 0; i < n; i++)
{
/* 获取数据域 */
int x;
scanf_s("%d", &x);
/* 为新建结点创建空间 */
LNode *p = (LNode *)malloc(sizeof(LNode));
p->data = x; /* 设置数据域 */
p->next = L->next; /* 插入的结点指针指向头结点指针所指区域 */
L->next = p; /* 头结点指针指向插入的元素 */
}
return L;
}头插法时,读入数据的顺序与生成链表中的元素顺序是相反的,每个结点插入时间为 $O(1)$ ,当表长为 $n$ 时,时间复杂度为 $O(n)$ 。
假设不存在头结点,则插入代码为:
LinkList InsertListFromHead(LinkList &L, int n)
{
/* 假设没有头结点 */
int x;
scanf_s("%d", &x);
/* 第一个元素的插入 */
L = (LinkList)malloc(sizeof(LNode));
L->data = x;
L->next = NULL;
/* 其余元素插入 */
for (int i = 1; i < n; i++)
{
/* 获取数据域 */
int x;
scanf_s("%d", &x);
/* 为插入结点创建空间 */
LNode *p = (LNode *)malloc(sizeof(LNode));
p->data = x;
p->next = L->next;
L->next = p;
}
return L;
} -
尾插法
LinkList InsertListFromTail(LinkList &L, int n)
{
/* 头结点 */
L = (LinkList)malloc(sizeof(LNode));
L->next = NULL;
/* 引入一个尾结点,初始化为与头结点相同的域 */
LNode *tail = L;
for (int i = 0; i < n; i++)
{
/* 获取数据域 */
int x;
scanf_s("%d", &x);
LNode *p = (LNode *)malloc(sizeof(LNode));
p->data = x;
/* 添加在 tail 后 */
p->next = tail->next;
tail->next = p;
/* tail = p,使得下一个插入结点能够在 p 之后 */
tail = p;
}
tail->next = NULL; // 尾结点指针置空
return L;
}时间复杂度为 $O(n)$ 。
按位序查找值
返回位序对应的结点的数据域
/* 按位序找到结点值 */ |
按值查找位序
按值查找位序,没有找到对应的值则返回0
/* 按值查找结点位序 */ |
按位序插入结点
/* 按位置插入结点 */ |
按位序删除结点
/* 按位序删除结点 */ |
获取表长
int GetLinkListLen(LinkList L) |
双链表的定义
单链表只有后继指针,只能向后遍历。访问后继结点的时间复杂度为 $O(1)$ ,访问前驱结点的时间复杂度为 $O(n)$ 。
双链表有前驱和后继指针,可以向前向后遍历。访问后继结点和前驱结点的时间复杂度都为 $O(1)$ 。
双链表上的操作
按顺序插入结点
/* 双链表 尾插法 */ |
按位序插入结点
/* 双链表 按位序插入结点 */ |
按位序删除结点
/* 双链表 根据位序删除结点 */ |
循环链表
-
循环单链表
- 最后一个结点的next指针指向头结点。在任何一个位置插入和删除结点的操作都是等价的,因此不需要判断是否为表尾结点。
- 可以从任何一个位置开始遍历整个链表。
- 对于循环单链表而言,通常设置的是尾指针,假设尾指针为
r,则r->next即为头指针。如果只有头指针,则对表尾操作需要 $O(n)$ 的时间,因为需要遍历过去,但是如果是尾指针,则对表头表尾操作都只需要 $O(1)$ 的时间。
Linklist InsertDataFromTail(Linklist &CL, int n)
{
CL = (Linklist)malloc(sizeof(LNode) * n);
CL->next = CL; /* 指向自己 */
LNode *tail = CL;
for (int i = 0; i < n; i++)
{
int x;
scanf_s("%d", &x);
LNode *insNode = (LNode *)malloc(sizeof(LNode));
insNode->data = x;
insNode->next = tail->next;
tail->next = insNode;
tail = insNode;
}
return CL;
}循环单链表的尾插法;
-
循环双链表
- 头结点的prior需要指向尾结点,尾结点的next需要指向头结点。
CL = (DLinklist)malloc(sizeof(DNode) * n);
CL->next = CL;
CL->prior = CL;
静态链表
借助数组来描述线性表的链式存储。
|
顺序表和链表的比较
性质比较
- 存取方式
- 顺序表:可以顺序存放,随机存取,仅需一次访问
- 链表:从表头依次存取,需要依次访问
- 逻辑结构与物理结构
- 顺序表:逻辑相邻的元素物理相邻
- 链表:逻辑相邻的元素不需要物理相邻
- 查找、插入和删除操作
- 查找:
- 按值查找:
- 顺序表:无序顺序表时间复杂度为 $O(n)$ ,有序顺序表采取折半法时间复杂度为 $O(log_2n)$ 。
- 链表:时间复杂度为 $O(n)$ 。
- 按位置查找:
- 顺序表:时间复杂度为 $O(1)$ 。
- 链表:时间复杂度为 $O(n)$ 。
- 按值查找:
- 插入和删除:
- 顺序表:平均需要移动半个表长的元素,所以最坏时间复杂度为:$O(n)$ 。
- 链表:时间复杂度为 $O(1)$ 。
- 查找:
- 空间分配
- 顺序表
- 静态分配:满了不能扩充,分配多了浪费空间
- 动态分配:可以扩充,但是需要移动大量元素,如果没有连续空间分配将失败
- 链表:只要有内存空间即可灵活分配。
- 顺序表
如何选取
- 基于存储考虑:难以估计长度和存储规模的时候,不要用顺序表,但是链式存储存储密度低
- 基于运算考虑:插入删除频繁时用链表,访问频繁时用顺序表
- 基于环境考虑:顺序表容易实现,链表操作基于指针。
课后题
|
